5 21 honeycomb

5₂₁ honeycomb
Type	Uniform honeycomb
Family	k₂₁ polytope
Schläfli symbol	{3,3,3,3,3,3^2,1}
Coxeter symbol	5₂₁
Coxeter-Dynkin diagram
8-faces	5₁₁ {3⁷}
7-faces	{3⁶}
6-faces	{3⁵}
5-faces	{3⁴}
4-faces	{3³}
Cells	{3²}
Faces	{3}
Cell figure	1₂₁
Face figure	2₂₁
Edge figure	3₂₁
Vertex figure	4₂₁
Symmetry group	${\tilde {E}}_{8}$ , [3^5,2,1]

In geometry, the 5₂₁ honeycomb is a uniform tessellation of 8-dimensional Euclidean space. The symbol 5₂₁ is from Coxeter, named for the length of the 3 branches of its Coxeter-Dynkin diagram.^[1]

This honeycomb was first studied by Gosset who called it a 9-ic semi-regular figure^[2] (Gosset regarded honeycombs in n dimensions as degenerate n+1 polytopes).

Each vertex of the 5₂₁ honeycomb is surrounded by 2160 8-orthoplexes and 17280 8-simplices.

The vertex figure of Gosset's honeycomb is the semiregular 4₂₁ polytope. It is the final figure in the k₂₁ family.

This honeycomb is highly regular in the sense that its symmetry group (the affine ${\tilde {E}}_{8}$ Weyl group) acts transitively on the k-faces for k ≤ 6. All of the k-faces for k ≤ 7 are simplices.

Construction

It is created by a Wythoff construction upon a set of 9 hyperplane mirrors in 8-dimensional space.

The facet information can be extracted from its Coxeter-Dynkin diagram.

Removing the node on the end of the 2-length branch leaves the 8-orthoplex, 6₁₁.

Removing the node on the end of the 1-length branch leaves the 8-simplex.

The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the 4₂₁ polytope.

The edge figure is determined from the vertex figure by removing the ringed node and ringing the neighboring node. This makes the 3₂₁ polytope.

The face figure is determined from the edge figure by removing the ringed node and ringing the neighboring node. This makes the 2₂₁ polytope.

The cell figure is determined from the face figure by removing the ringed node and ringing the neighboring node. This makes the 1₂₁ polytope.

Kissing number

Each vertex of this tessellation is the center of a 7-sphere in the densest known packing in 8 dimensions; its kissing number is 240, represented by the vertices of its vertex figure 4₂₁.

E8 lattice

${\tilde {E}}_{8}$ contains ${{\tilde {A}}}_{8}$ as a subgroup of index 5760.^[3] Both ${\tilde {E}}_{8}$ and ${{\tilde {A}}}_{8}$ can be seen as affine extensions of $A_{8}$ from different nodes:

${\tilde {E}}_{8}$ contains ${{\tilde {D}}}_{8}$ as a subgroup of index 270.^[4] Both ${\tilde {E}}_{8}$ and ${{\tilde {D}}}_{8}$ can be seen as affine extensions of $D_{8}$ from different nodes:

The vertex arrangement of 5₂₁ is called the E8 lattice.^[5]

The E8 lattice can also be constructed as a union of the vertices of two 8-demicube honeycombs (called a D₈² or D₈⁺ lattice), as well as the union of the vertices of three 8-simplex honeycombs (called an A₈³ lattice):

∪

Regular complex honeycomb

Using a complex number coordinate system, it can also be constructed as a $\mathbb {C} ^{4}$ regular complex polytope, given the symbol 3{3}3{3}3{3}3{3}3, and Coxeter diagram .^[6] Its elements are in relative proportion as 1 vertex, 80 3-edges, 270 ₃{3}₃ faces, and 1 ₃{3}₃{3}₃{3}₃ Witting polytope cells.

Related polytopes and honeycombs

The 5₂₁ is seventh in a dimensional series of semiregular polytopes, identified in 1900 by Thorold Gosset. Each member of the sequence has the previous member as its vertex figure. All facets of these polytopes are regular polytopes, namely simplexes and orthoplexes.

k₂₁ figures in n dimensional
Space	Finite						Euclidean	Hyperbolic
E_n	3	4	5	6	7	8	9	10
Coxeter group	E₃=A₂A₁	E₄=A₄	E₅=D₅	E₆	E₇	E₈	E₉ = ${\tilde {E}}_{8}$ = E₈⁺	E₁₀ = ${\bar {T}}_{8}$ = E₈⁺⁺
Coxeter diagram
Symmetry	[3^−1,2,1]	[3^0,2,1]	[3^1,2,1]	[3^2,2,1]	[3^3,2,1]	[3^4,2,1]	[3^5,2,1]	[3^6,2,1]
Order	12	120	192	51,840	2,903,040	696,729,600	∞
Graph							-	-
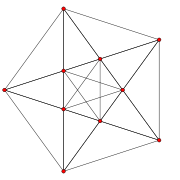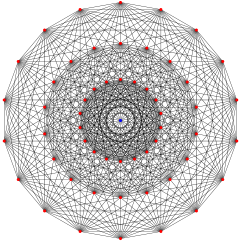Name	−1₂₁	0₂₁	1₂₁	2₂₁	3₂₁	4₂₁	5₂₁	6₂₁

Notes

↑ Coxeter, 1973, Chapter 5: The Kaleidoscope
↑ Gosset, Thorold (1900). "On the regular and semi-regular figures in space of n dimensions". Messenger of Mathematics. 29: 43–48.
↑ N.W. Johnson: Geometries and Transformations, Manuscript, (2011) Chapter 12: Euclidean symmetry groups, p 177
↑ Johnson (2011) p.177
↑ http://www.math.rwth-aachen.de/~Gabriele.Nebe/LATTICES/E8.html
↑ Coxeter Regular Convex Polytopes, 12.5 The Witting polytope

References

Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
Coxeter, H. S. M. (1973). Regular Polytopes ((3rd ed.) ed.). New York: Dover Publications. ISBN 0-486-61480-8.
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
N.W. Johnson: Geometries and Transformations, (2015)

Fundamental convex regular and uniform honeycombs in dimensions 3–10 (or 2-9)
Family	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
Uniform tiling	{3^[3]}	δ₃	hδ₃	qδ₃	Hexagonal
Uniform convex honeycomb	{3^[4]}	δ₄	hδ₄	qδ₄
Uniform 5-honeycomb	{3^[5]}	δ₅	hδ₅	qδ₅	24-cell honeycomb
Uniform 6-honeycomb	{3^[6]}	δ₆	hδ₆	qδ₆
Uniform 7-honeycomb	{3^[7]}	δ₇	hδ₇	qδ₇	2₂₂
Uniform 8-honeycomb	{3^[8]}	δ₈	hδ₈	qδ₈	1₃₃ • 3₃₁
Uniform 9-honeycomb	{3^[9]}	δ₉	hδ₉	qδ₉	1₅₂ • 2₅₁ • 5₂₁
Uniform 10-honeycomb	{3^[10]}	δ₁₀	hδ₁₀	qδ₁₀
Uniform n-honeycomb	{3^[n]}	δ_n	hδ_n	qδ_n	1_k2 • 2_k1 • k₂₁

This article is issued from Wikipedia - version of the 10/23/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.