Achilles number
An Achilles number is a number that is powerful but not a perfect power.[1] A positive integer n is a powerful number if, for every prime factor p of n, p2 is also a divisor. In other words, every prime factor appears at least squared in the factorization. All Achilles numbers are powerful. However, not all powerful numbers are Achilles numbers: only those that cannot be represented as mk, where m and k are positive integers greater than 1.
Achilles numbers were named by Henry Bottomley after Achilles, a hero of the Trojan war, who was also powerful but imperfect. Strong Achilles numbers are Achilles numbers whose Euler totients are also Achilles numbers.[2]
Sequence of Achilles numbers
A number n = p1a1 p2a2 … pkak is powerful if min(a1, a2, …, ak) ≥ 2. If in addition gcd(a1, a2, …, ak) = 1 the number is an Achilles number.
The Achilles numbers up to 5000 are:
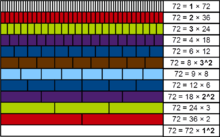
- 72, 108, 200, 288, 392, 432, 500, 648, 675, 800, 864, 968, 972, 1125, 1152, 1323, 1352, 1372, 1568, 1800, 1944, 2000, 2312, 2592, 2700, 2888, 3087, 3200, 3267, 3456, 3528, 3872, 3888, 4000, 4232, 4500, 4563, 4608, 5000 (sequence A052486 in the OEIS).
The smallest pair of consecutive Achilles numbers is:[3]
- 5425069447 = 73 × 412 × 972
- 5425069448 = 23 × 260412
Examples
108 is a powerful number. Its prime factorization is 22 · 33, and thus its prime factors are 2 and 3. Both 22 = 4 and 32 = 9 are divisors of 108. However, 108 cannot be represented as mk, where m and k are positive integers greater than 1, so 108 is an Achilles number.
360 is not an Achilles number because it is not powerful. One of its prime factors is 5 but 360 is not divisible by 52 = 25.
Finally, 784 is not an Achilles number. It is a powerful number, because not only are 2 and 7 its only prime factors, but also 22 = 4 and 72 = 49 are divisors of it. Nonetheless, it is a perfect power:
So it is not an Achilles number.
References
- ↑ Weisstein, Eric W. "Achilles Number". MathWorld.
- ↑ Project Euler problem 302
- ↑ Carlos Rivera, The Prime Puzzles and Problem Connection, Problem 53