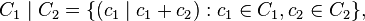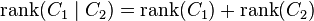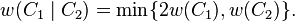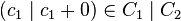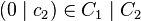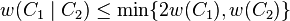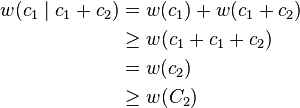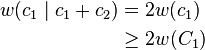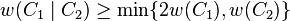Bar product
In information theory, the bar product of two linear codes C2 ⊆ C1 is defined as
where (a | b) denotes the concatenation of a and b. If the code words in C1 are of length n, then the code words in C1 | C2 are of length 2n.
The bar product is an especially convenient way of expressing the Reed–Muller RM (d, r) code in terms of the Reed–Muller codes RM (d − 1, r) and RM (d − 1, r − 1).
The bar product is also referred to as the | u | u+v | construction[1] or (u | u + v) construction.[2]
Properties
Rank
The rank of the bar product is the sum of the two ranks:
Proof
Let 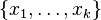 be a basis for
be a basis for 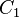 and let
and let  be a basis for
be a basis for 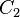 . Then the set
. Then the set
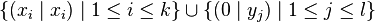
is a basis for the bar product 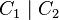 .
.
Hamming weight
The Hamming weight w of the bar product is the lesser of (a) twice the weight of C1, and (b) the weight of C2:
Proof
For all 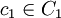 ,
,
which has weight 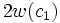 . Equally
. Equally
for all 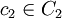 and has weight
and has weight 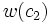 . So minimising over
. So minimising over 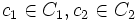 we have
we have
Now let 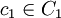 and
and 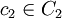 , not both zero. If
, not both zero. If 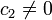 then:
then:
If 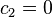 then
then
so
See also
References
- ↑ F.J. MacWilliams; N.J.A. Sloane (1977). The Theory of Error-Correcting Codes. North-Holland. p. 76. ISBN 0-444-85193-3.
- ↑ J.H. van Lint (1992). Introduction to Coding Theory. GTM 86 (2nd ed.). Springer-Verlag. p. 47. ISBN 3-540-54894-7.