Butterfly theorem

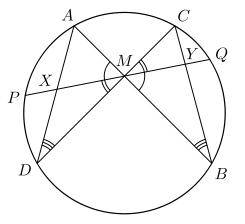
The butterfly theorem is a classical result in Euclidean geometry, which can be stated as follows:^{[1]:p. 78}

Let M be the midpoint of a chord PQ of a circle, through which two other chords AB and CD are drawn; AD and BC intersect chord PQ at X and Y correspondingly. Then M is the midpoint of XY.

Proof

A formal proof of the theorem is as follows: Let the perpendiculars XX′ and XX″ be dropped from the point X on the straight lines AM and DM respectively. Similarly, let YY′ and YY″ be dropped from the point Y perpendicular to the straight lines BM and CM respectively.

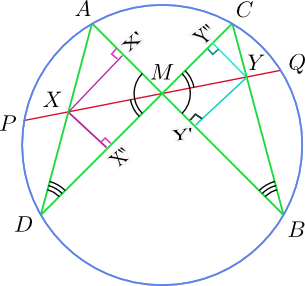
Now, since

$\triangle MXX'\sim \triangle MYY',\,$

${MX \over MY}={XX' \over YY'},$

$\triangle MXX''\sim \triangle MYY'',\,$

${MX \over MY}={XX'' \over YY''},$

$\triangle AXX'\sim \triangle CYY'',\,$

${XX' \over YY''}={AX \over CY},$

$\triangle DXX''\sim \triangle BYY',\,$

${XX'' \over YY'}={DX \over BY},$

From the preceding equations, it can be easily seen that

$\left({MX \over MY}\right)^{2}={XX' \over YY'}{XX'' \over YY''},$

${\displaystyle {}={AX\cdot DX \over CY\cdot BY},}$

${\displaystyle {}={PX\cdot QX \over PY\cdot QY},}$

${\displaystyle {}={(PM-XM)\cdot (MQ+XM) \over (PM+MY)\cdot (QM-MY)},}$

${}={(PM)^{2}-(MX)^{2} \over (PM)^{2}-(MY)^{2}},$

since PM = MQ.

Now,

${(MX)^{2} \over (MY)^{2}}={(PM)^{2}-(MX)^{2} \over (PM)^{2}-(MY)^{2}}.$

So, it can be concluded that MX = MY, or M is the midpoint of XY.

Other proofs exist,^[2] including one using projective geometry.^[3]

History

Proving the butterfly theorem was posed as a problem by William Wallace in The Gentlemen's Mathematical Companion (1803). Three solutions were published in 1804, and in 1805 Sir William Herschel posed the question again in a letter to Wallace. Rev. Thomas Scurr asked the same question again in 1814 in the Gentlemen's Diary or Mathematical Repository.^[4]

References

1. Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).
2. Martin Celli, "A Proof of the Butterfly Theorem Using the Similarity Factor of the Two Wings", Forum Geometricorum 16, 2016, 337–338. http://forumgeom.fau.edu/FG2016volume16/FG201641.pdf
3. , problem 8.
4. William Wallace's 1803 Statement of the Butterfly Theorem, cut-the-knot, retrieved 2015-05-07.

External links

• The Butterfly Theorem at cut-the-knot
• A Better Butterfly Theorem at cut-the-knot
• Proof of Butterfly Theorem at PlanetMath
• The Butterfly Theorem by Jay Warendorff, the Wolfram Demonstrations Project.
• Weisstein, Eric W. "Butterfly Theorem". MathWorld.