Coin rotation paradox
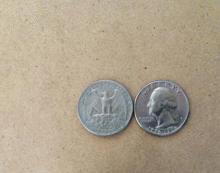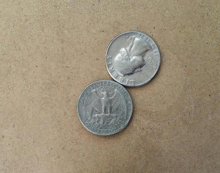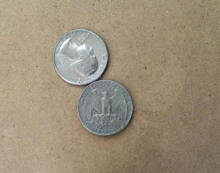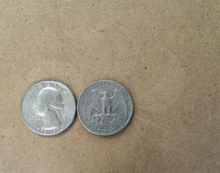
The coin rotation paradox is the counter-intuitive observation that, when one coin is rolled around the rim of another coin of equal size, the moving coin completes one full rotation after only going half the way around the stationary coin.
Description
The problem begins with two identical coins. One is rotated around the other without slipping so that it ends up on the opposite side of the other coin from where it began. It has made a single rotation, yet has only rolled a distance equal to half of its circumference.
This can be visualised by placing two coins that are touching each other at one point flat on a table. Let both of them have the heads side up and be parallel to each other. Now keeping one coin stationary, rotate the other coin such that there is always one point of contact. Rotate until it reaches the opposite side. Now the coins will be again parallel to each other, contrary to our intuition.
Solution
The rolling coin actually participates in two separate motions not unlike the moon relative to the earth:
- It rotates around its own center.
- It revolves around the center of the other coin.
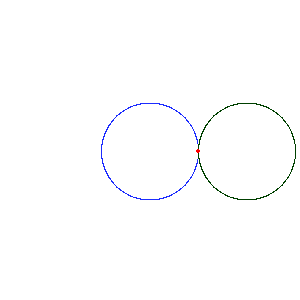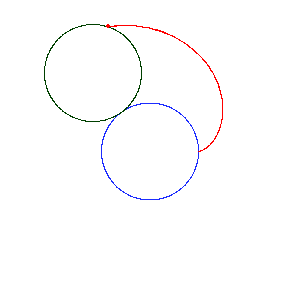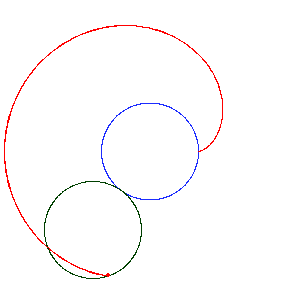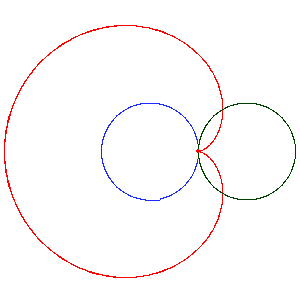
The point of contact on both the stationary coin and the rotating coin must move the same distance, half the circumference of the coin. For example, the point of contact has moved from its right side to its left side. Correspondingly, the point of contact on the rotating coin must move from its left side to its right side. This means the rotating coin has made one full rotation about its own center while its center has made one half revolution about the stationary coin.
Another intuitive way of approaching this problem would be to imagine what happens when a block slides over a circle without any inherent rotation of its own. It is seen that the block does 1 rotation purely due to its revolution around the circle. Thus, the revolution always adds an extra rotation, irrespective of the size of the circles or coins.
