Compound of two icosahedra
| Compound of two icosahedra | |
|---|---|
 | |
| Type | Uniform compound |
| Index | UC46 |
| Schläfli symbols | β{3,4} βr{3,3} |
| Coxeter diagrams | |
| Polyhedra | 2 icosahedra |
| Faces | 16+24 triangles |
| Edges | 60 |
| Vertices | 24 |
| Symmetry group | octahedral (Oh) |
| Subgroup restricting to one constituent | pyritohedral (Th) |
This uniform polyhedron compound is a composition of 2 icosahedra. It has octahedral symmetry Oh. As a holosnub, it is represented by Schläfli symbol β{3,4} and Coxeter diagram ![]()
![]()
![]()
![]()
![]() .
.
The triangles in this compound decompose into two orbits under action of the symmetry group: 16 of the triangles lie in coplanar pairs in octahedral planes, while the other 24 lie in unique planes.
It shares the same vertex arrangement as a nonuniform truncated octahedron, having irregular hexagons alternating with long and short edges.
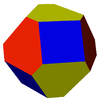  Nonuniform and uniform truncated octahedra. The first shares its vertex arrangement with this compound. |
The icosahedron, as a uniform snub tetrahedron![]() , is similar to these snub-pair compounds: compound of two snub cubes and compound of two snub dodecahedra.
, is similar to these snub-pair compounds: compound of two snub cubes and compound of two snub dodecahedra.
Cartesian coordinates
Cartesian coordinates for the vertices of this compound are all the permutations of
- (±1, 0, ±τ)
where τ = (1+√5)/2 is the golden ratio (sometimes written φ).
Compound of two dodecahedra
The dual compound has two dodecahedra as pyritohedrons in dual positions:
References
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.
External links
- VRML model:
