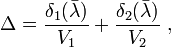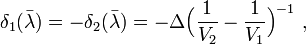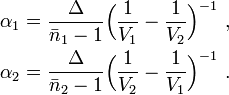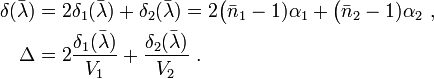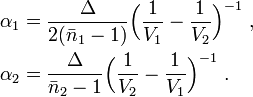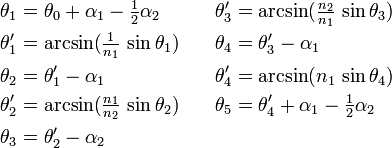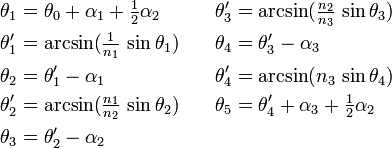Compound prism
A compound prism is a set of multiple triangular prism elements placed in contact, and often cemented together to form a solid assembly.[1] The use of multiple elements gives several advantages to an optical designer:[2]
- One can achieve spectral dispersion without causing the deviation of the beam at the design wavelength. Thus, light at the design wavelength which enters at an angle
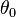 with respect to the optical axis, exits the prism at the same angle with respect to the same axis. This kind of effect is often called "direct vision dispersion" or "nondeviating dispersion".[3]
with respect to the optical axis, exits the prism at the same angle with respect to the same axis. This kind of effect is often called "direct vision dispersion" or "nondeviating dispersion".[3] - One can achieve deviation of the incident beam while also greatly reducing the dispersion introduced into the beam: an achromatic deflecting prism. This effect is used in beam steering.[4][5]
- One can tune the prism dispersion to achieve greater dispersion linearity or to achieve higher-order dispersion effects.
Doublet
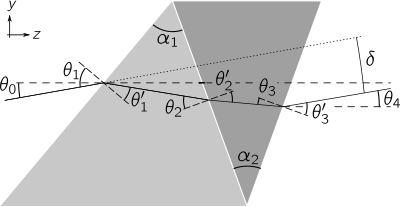
The simplest compound prism is a doublet, consisting of two elements in contact, as shown in the figure at right. A ray of light passing through the prism is refracted at the first air-glass interface, again at the interface between the two glasses, and a final time at the exiting glass-air interface. The deviation angle 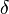 of the ray is given by the difference in ray angle between the incident ray and the exiting ray:
of the ray is given by the difference in ray angle between the incident ray and the exiting ray: 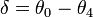 . While one can produce direct vision dispersion from doublet prisms, there is typically significant displacement of the beam (shown as a separation between the two dashed horizontal lines in the y direction). Mathematically, one can calculate
. While one can produce direct vision dispersion from doublet prisms, there is typically significant displacement of the beam (shown as a separation between the two dashed horizontal lines in the y direction). Mathematically, one can calculate 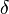 by concatenating the Snell's law equations at each interface,[2]
by concatenating the Snell's law equations at each interface,[2]
so that the deviation angle is a nonlinear function of the glass refractive indices 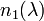 and
and 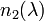 , the prism elements' apex angles
, the prism elements' apex angles 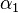 and
and 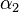 , and the angle of incidence
, and the angle of incidence 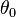 of the ray. Note that
of the ray. Note that 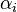 indicates that the prism is inverted (the apex points downward).
indicates that the prism is inverted (the apex points downward).
If the angle of incidence 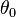 and prism apex angle
and prism apex angle 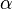 are both small, then
are both small, then 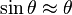 and
and 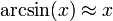 , so that the nonlinear equation in the deviation angle
, so that the nonlinear equation in the deviation angle 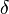 can be approximated by the linear form
can be approximated by the linear form
(See also Prism deviation angle and dispersion.) If we further assume that the wavelength dependence to the refractive index is approximately linear, then the dispersion can be written as
where 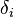 and
and 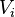 are the dispersion and Abbe number of element
are the dispersion and Abbe number of element 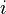 within the compound prism,
within the compound prism, 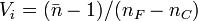 . The central wavelength of the spectrum is denoted
. The central wavelength of the spectrum is denoted 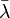 .
.
Doublet prisms are often used for direct-vision dispersion. In order to design such a prism, we let 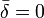 , and simultaneously solving equations
, and simultaneously solving equations 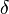 and
and 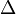 gives
gives
from which one can obtain the element apex angles 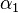 and
and 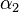 from the mean refractive indices of the glasses chosen:
from the mean refractive indices of the glasses chosen:
Note that this formula is only accurate under the small angle approximation.
Double-Amici
While the doublet prism is the simplest compound prism type, the double-Amici prism is much more common. This prism is a three-element system (a triplet), in which the first and third elements share both the same glass and the same apex angles. The design layout is thus symmetric about the plane passing through the center of its second element. Due to its symmetry, the linear design equations (under the small angle approximation) for the double-Amici prism differ from those of the doublet prism only by a factor of 2 in front of the first term in each equation:[2]

Thus, we can derive the expressions for the prism angles using these linear equations, giving
The exact nonlinear equation for the deviation angle 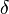 is obtained by concatenating the refraction equations obtained at each interface:
is obtained by concatenating the refraction equations obtained at each interface:
The ray deviation angle is given by 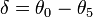 .
.
Triplet
The double-Amici prism is a symmetric form of the more general triplet prism, in which the apex angles and glasses of the two outer elements may differ (see the figure at right). Although triplet prisms are rarely found in optical systems, their added degrees of freedom beyond the double-Amici design allow for improved dispersion linearity. The deviation angle of the triplet prism is obtained by concatenating the refraction equations at each interface:[6][7]
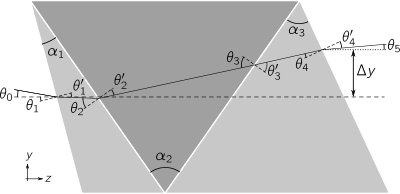
Here too the ray deviation angle is given by 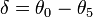 .
.
See also
References
- ↑ John Browning, "Note on the use of compound prisms," MNRAS 31: 203-205 (1871).
- 1 2 3 Nathan Hagen and Tomasz S. Tkaczyk, "Compound prism design principles, I," Appl. Opt. 50: 4998-5011 (2011).
- ↑ Charles G. Abbott and Frederick E. Fowle, Jr., "A prism of uniform dispersion," Astrophys. J. 11: 135-139 (1900).
- ↑ Bradley D. Duncan, Philip J. Bos, and Vassili Sergan, "Wide-angle achromatic prism beam steering for infrared countermeasure applications," Opt. Eng 42: 1038-1047 (2003).
- ↑ Zhilin Hu and Andrew M. Rollins, "Fourier domain optical coherence tomography with a linear-in-wavenumber spectrometer," Opt. Lett. 32: 3525-3527 (2007).
- ↑ Nathan Hagen and Tomasz S. Tkaczyk, "Compound prism design principles, II: triplet and Janssen prisms," Appl. Opt. 50: 5012-5022 (2011).
- ↑ Nathan Hagen and Tomasz S. Tkaczyk, "Compound prism design principles, III: linear-in-wavenumber and optical coherence tomography prisms," Appl. Opt. 50: 5023-5030 (2011).
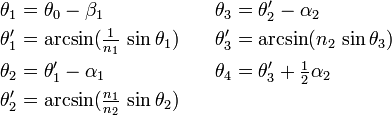
![\delta (\lambda) = \big[ n_1 (\lambda - 1 \big] \alpha_1 + \big[ n_2 (\lambda) - 1 \big] \alpha_2 \ .](../I/m/4d46f4eaa111dd9aaf01e23e8b5899b0.png)