Crash simulation

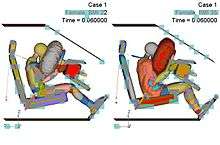
A crash simulation with a slender (left) and obese (right) female passenger.

A crash simulation is a virtual recreation of a destructive crash test of a car or a highway guard rail system using a computer simulation in order to examine the level of safety of the car and its occupants. Crash simulations are used by automakers during computer-aided engineering (CAE) analysis for crashworthiness in the computer-aided design (CAD) process of modelling new cars. During a crash simulation, the kinetic energy, or energy of motion, that a vehicle has before the impact is transformed into deformation energy, mostly by plastic deformation (plasticity) of the car body material (Body in White), at the end of the impact.

Data obtained from a crash simulation indicate the capability of the car body or guard rail structure to protect the vehicle occupants during a collision (and also pedestrians hit by a car) against injury. Important results are the deformations (for example, steering wheel intrusions) of the occupant space (driver, passengers) and the decelerations (for example, head acceleration) felt by them, which must fall below threshold values fixed in legal car safety regulations. To model real crash tests, today's crash simulations include virtual models of crash test dummies and of passive safety devices (seat belts, airbags, shock absorbing dash boards, etc.). Guide rail tests evaluate vehicle deceleration and rollover potential, as well as penetration of the barrier by vehicles.

Origin

In the years 1970 attempts were made to simulate car crash events with non-linear spring-mass systems after calibration, which require as an input the results of physical destructive laboratory tests, needed to determine the mechanical crushing behavior of each spring component of the modeled system. "First principle" simulations like more elaborate finite element models, however, need only the definition of the structural geometry and the basic material properties (rheology of car body steel, glass, plastic parts, etc.) as an input to generate the numerical model.

The origins of industrial first principle computerized car crash simulation lie in military defense, outer space and civil nuclear power plant applications. Upon presentation of a simulation of the accidental crash of a military fighter plane into a nuclear power plant on May 30, 1978 by ESI Group in a meeting organized by the Verein Deutscher Ingenieure (VDI) in Stuttgart, car makers became alerted to the possibility of using this technology for the simulation of destructive car crash tests (Haug 1981).

The first successful frontal full car crash simulation: a Volkswagen Polo collided with a rigid concrete barrier at 50 km/h (ESI 1986).

In the following years, German car makers produced more complex crash simulation studies, simulating the crash behavior of individual car body components, component assemblies, and quarter and half car bodies in white (BIW). These experiments culminated in a joint project by the Forschungsgemeinschaft Automobil-Technik (FAT), a conglomeration of all seven German car makers (Audi, BMW, Ford, Mercedes-Benz, Opel, Porsche, and Volkswagen), which tested the applicability of two emerging commercial crash simulation codes. These simulation codes recreated a frontal impact of a full passenger car structure (Haug 1986) and they ran to completion on a computer overnight. Now that turn-around time between two consecutive job-submissions (computer runs) did not exceed one day, engineers were able to make efficient and progressive improvements of the crash behavior of the analyzed car body structure.

Application

Crash simulations are used to investigate the safety of the car occupants during impacts on the front end structure of the car in a "head-on collision" or "frontal impact", the lateral structure of the car in a “side collision” or “side impact”, the rear end structure of a car in a "rear-end collision" or “rear impact”, and the roof structure of the car when it overturns during a "rollover". Crash simulations can also be used to assess injury to pedestrians hit by a car.

Benefits

A crash simulation produces results without actual destructive testing of a new car model. This way, tests can be performed quickly and inexpensively in a computer, which permits optimization of the design before a real prototype of the car has been manufactured. Using a simulation, problems can be solved before spending time and money on an actual crash test. The great flexibility of printed output and graphical display enables designers to solve some problems that would have been nearly impossible without the help of a computer.

Analysis

A subdivision of the metal exterior of the car, called a finite element, is connected to nodes at each vertex.

Large number of crash simulations use a method of analysis called the Finite Element Method. The complex problems are solved by dividing a surface into a large but still finite number of elements and determining the motion of these elements over very small periods of time. Another approach to crash simulations is performed by application of Macro Element Method. The difference between two mentioned above methodologies is that the structure in case of Macro Element Method consists of smaller number of elements. The calculation algorithm of structure deformation is based on experimental data rather than calculated from partial differential equations.

Pam-Crash started crash simulation and together with LS-DYNA is a software package which is widely used for application of Finite Element Method. This method allows detailed modeling of a structure, but the disadvantage lies in high processing unit requirements and calculation time. The Visual Crash Studio uses Macro Element Methodology. In comparison with FEM it has some modeling and boundary condition limitations but its application does not require advanced computers and the calculation time is incomparably smaller. Two presented methods complement each other. Macro Element Method is useful at early stage of the structure design process while Finite Element Method performs well at its final stages.

Structural analysis

In a typical crash simulation, the car body structure is analyzed using spatial discretization, that is, breaking up the continuous movement of the body in real time into smaller changes in position over small, discrete time steps. The discretization involves subdividing the surface of the constituent, thin, sheet metal parts into a large number (approaching one million in 2006) of quadrilateral or triangular regions, each of which spans the area between "nodes" to which its corners are fixed. Each element has mass, which is distributed as concentrated masses and as mass moments of inertia to its connecting nodes. Each node has 6 kinematic degrees of freedom, that is, one node can move in three linear directions under translation and can rotate about three independent axes. The spatial coordinates (x), displacement (u), velocity (v), and acceleration (a) of each node is mostly expressed in a three-dimensional rectangular Cartesian coordinate system with axes X,Y, and Z.

If the nodes move during a crash simulation, the connected elements move, stretch, and bend with their nodes, which causes them to impart forces and moments to their nodal connections. The forces and moments at the nodes correspond to the inertia forces and moments, caused by their translational (linear) and angular accelerations and to the forces and moments transmitted by the resistance of the structural material of the connected elements as they deform. Sometimes, additional external structural loads are applied, like gravity loads from the self weight of the parts, or added loads from external masses.

The forces and moments of all nodes are collected into a column vector (or column matrix), and the time dependent equations of motion (in dynamic equilibrium) can be written as follows.

${\displaystyle \mathbf {Ma} =\mathbf {F} _{ext}-\mathbf {F} _{int}}$

where vector ${\displaystyle \mathbf {Ma} }$ (mass times acceleration vector) collects the inertia forces at the nodes, ${\displaystyle \mathbf {F} _{ext}}$ collects the external nodal loads, and ${\displaystyle \mathbf {F} _{int}}$ collects the internal resisting forces from the deformation of the material. M is a diagonal matrix of the nodal masses. Each vector (u, v, a, F, etc.) has dimension 6 times the total number of nodes in the crash model (about 6 million “degrees of freedom” for every 1 million "nodes" in 3-D thin shell finite element models).

Time analysis

A crash simulation uses time discretization as well to separate the continuous changes in time into very small, usable segments. The dynamic equations of motion hold at all times during a crash simulation and must be integrated in time, t, starting from an initial condition at time zero, which is just prior to the crash. According to the explicit finite difference time integration method used by most crash codes, the accelerations, velocities, and displacements of the body are related by the following equations.

${\displaystyle \mathbf {a} _{n}=\mathbf {M} ^{-1}(\mathbf {F} _{ext}-\mathbf {F} _{int})_{n}}$

${\displaystyle \mathbf {v} _{n+1/2}=\mathbf {v} _{n-1/2}+\mathbf {a} _{n}\Delta t_{n}}$

${\displaystyle \mathbf {u} _{n+1}=\mathbf {u} _{n}+\mathbf {v} _{n+1/2}\Delta t_{n+1/2}}$

In these equations the subscripts n±1/2, n, n+1 denote past, present, and future times, t, at half and full-time intervals with time steps ${\displaystyle \Delta t_{n}}$ and ${\displaystyle \Delta t_{n+1/2}}$, respectively.

Solution

The above system of linear equations is solved for the accelerations, ${\displaystyle \mathbf {a} _{n}}$, the velocities, ${\displaystyle \mathbf {v} _{n+1/2}}$, and the displacements, ${\displaystyle \mathbf {u} _{n+1}}$, at each discrete point in time, t, during the crash duration. This solution is trivial, since the mass matrix is diagonal. The computer time is proportional to the number of finite elements and the number of solution time steps. The stable solution time step, $\Delta t$, is limited for numerical stability, as expressed by the Courant–Friedrichs–Lewy condition (CFL), which states that “in any time-marching computer simulation, the time step must be less than the time for some significant action to occur, and preferably considerably less." In a crash simulation, the fastest significant actions are the acoustic signals that travel inside the structural material.

The solid elastic stress wave speed amounts to

${\displaystyle c={\sqrt {E_{0}/\rho }}}$

where $E_{0}$ is the initial elastic modulus (before plastic deformation) of the material and $\rho$ is the mass density. The largest stable time step for a given material is therefore

${\displaystyle \Delta t=d_{min}{\sqrt {\rho /E_{0}}}}$,

where $d_{min}$ is the smallest distance between any two nodes of the numerical crash simulation model.

Since this distance can change during a simulation, the stable time step changes and must be updated continually as the solution proceeds in time. When using steel, the typical value of the stable time step is about one microsecond when the smallest discrete node distance in the mesh of the finite element model is about 5 millimeters. It needs then more than 100,000 time intervals to solve a crash event that lasts for one tenth of a second. This figure is exceeded in many industrial crash models demanding optimized crash solvers with High-Performance Computing (HPC) features, such as vectorization and parallel computing.

See also

• Finite element method in structural mechanics
• Finite element analysis
• Crash test

References

• Haug, E. (1981) "Engineering safety analysis via destructive numerical experiments", EUROMECH 121, Polish Academy of Sciences, Engineering Transactions 29(1), 39–49.
• Haug, E., T. Scharnhorst, P. Du Bois (1986) "FEM-Crash, Berechnung eines Fahrzeugfrontalaufpralls", VDI Berichte 613, 479–505.