Del in cylindrical and spherical coordinates
| | Help resolve this verification problem at Wikiversity. |
This is a list of some vector calculus formulae for working with common curvilinear coordinate systems.
Notes
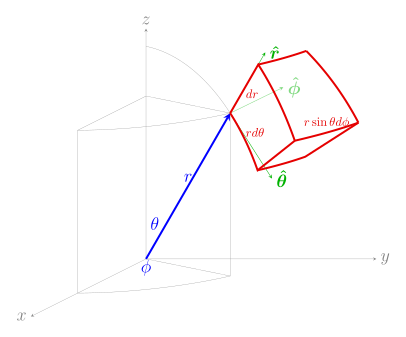
- This article uses the standard notation ISO 80000-2, which supersedes ISO 31-11, for spherical coordinates (other sources may reverse the definitions of θ and φ):
- The polar angle is denoted by θ: it is the angle between the z-axis and the radial vector connecting the origin to the point in question.
- The azimuthal angle is denoted by φ: it is the angle between the x-axis and the projection of the radial vector onto the xy-plane.
- The function atan2(y, x) can be used instead of the mathematical function arctan(y/x) owing to its domain and image. The classical arctan function has an image of (−π/2, +π/2), whereas atan2 is defined to have an image of (−π, π].
Coordinate conversions
| From | ||||
|---|---|---|---|---|
| Cartesian | Cylindrical | Spherical | ||
| To | Cartesian | N/A | ||
| Cylindrical | N/A | |||
| Spherical | N/A | |||
Unit vector conversions
| Cartesian | Cylindrical | Spherical | |
|---|---|---|---|
| Cartesian | N/A | ||
| Cylindrical | N/A | ||
| Spherical | N/A |
| Cartesian | Cylindrical | Spherical | |
|---|---|---|---|
| Cartesian | N/A | ||
| Cylindrical | N/A | ||
| Spherical | N/A |
Del formula
| Operation | Cartesian coordinates (x, y, z) | Cylindrical coordinates (ρ, φ, z) | Spherical coordinates (r, θ, φ), where θ is the polar angle and φ is azimuthal |
|---|---|---|---|
| A vector field A | |||
| Gradient ∇f | |||
| Divergence ∇ ⋅ A | |||
| Curl ∇ × A | |||
| Laplace operator ∇2f ≡ ∆f | |||
| Vector Laplacian ∇2A ≡ ∆A | |
| |
| Material derivativeα[1] (A ⋅ ∇)B | |
| |
| Tensor divergence ∇ ⋅ T | |
|
|
| Differential displacement dℓ | |||
| Differential normal area dS | |||
| Differential volume dV |
- ^α The source that is used for these formulae uses for the azimuthal angle and for the polar angle, which is common mathematical notation. This page uses for the polar angle and for the azimuthal angle, which is common notation in physics. In order to get the mathematics formulae, switch and in the formulae shown in the table above.
Non-trivial calculation rules
- (Lagrange's formula for del)
Cartesian derivation

The expressions for and are found in the same way.
Cylindrical derivation

Spherical derivation
See also
- Del
- Orthogonal coordinates
- Curvilinear coordinates
- Vector fields in cylindrical and spherical coordinates
References
- ↑ Weisstein, Eric W. "Convective Operator". Mathworld. Retrieved 23 March 2011.
External links
- Maxima Computer Algebra system scripts to generate some of these operators in cylindrical and spherical coordinates.
This article is issued from Wikipedia - version of the 11/6/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.