Diagonal intersection
Diagonal intersection is a term used in mathematics, especially in set theory.
If 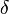 is an ordinal number and
is an ordinal number and 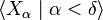 is a sequence of subsets of
is a sequence of subsets of 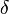 , then the diagonal intersection, denoted by
, then the diagonal intersection, denoted by
is defined to be
That is, an ordinal  is in the diagonal intersection
is in the diagonal intersection  if and only if it is contained in the first
if and only if it is contained in the first  members of the sequence. This is the same as
members of the sequence. This is the same as
where the closed interval from 0 to 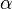 is used to
avoid restricting the range of the intersection.
is used to
avoid restricting the range of the intersection.
See also
References
- Thomas Jech, Set Theory, The Third Millennium Edition, Springer-Verlag Berlin Heidelberg New York, 2003, page 92.
- Akihiro Kanamori, The Higher Infinite, Second Edition, Springer-Verlag Berlin Heidelberg, 2009, page 2.
This article incorporates material from diagonal intersection on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
This article is issued from Wikipedia - version of the 3/7/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.


![\displaystyle\bigcap_{\alpha < \delta} ( [0, \alpha] \cup X_\alpha ),](../I/m/9cd938bd398b2d9901b0d24eabaa9ece.png)