Diamond graph

Diamond graph
Vertices 4
Edges 5
Radius 1
Diameter 2
Girth 3
Automorphisms 4 (Z/2Z×Z/2Z)
Chromatic number 3
Chromatic index 3
Properties Hamiltonian
Planar
Unit distance

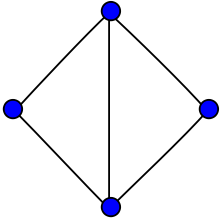
In the mathematical field of graph theory, the diamond graph is a planar undirected graph with 4 vertices and 5 edges.[1][2] It consists of a complete graph minus one edge.

The diamond graph has radius 1, diameter 2, girth 3, chromatic number 3 and chromatic index 3. It is also a 2-vertex-connected and a 2-edge-connected graceful[3] Hamiltonian graph.

Diamond-free graphs and forbidden minor

A graph is diamond-free if it has no diamond as an induced subgraph. The triangle-free graphs are diamond-free graphs, since every diamond contains a triangle. The diamond-free graphs are locally clustered: that is, they are the graphs in which every neighborhood is a cluster graph.

The family of graphs in which each connected component is a cactus graph is downwardly closed under graph minor operations. This graph family may be characterized by a single forbidden minor. This minor is the diamond graph.[4]

If both the butterfly graph and the diamond graph are forbidden minors, the family of graphs obtained is the family of pseudoforests.

Algebraic properties

The full automorphism group of the diamond graph is a group of order 4 isomorphic to the Klein four-group, the direct product of the cyclic group Z/2Z with itself.

The characteristic polynomial of the diamond graph is . It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.

See also

References

  1. ↑ Weisstein, Eric W. "Diamond Graph". MathWorld.
  2. ↑ ISGCI: Information System on Graph Classes and their Inclusions "List of Small Graphs".
  3. ↑ Sin-Min Lee, Y.C. Pan and Ming-Chen Tsai. "On Vertex-graceful (p,p+l)-Graphs".
  4. ↑ El-Mallah, Ehab; Colbourn, Charles J. (1988), "The complexity of some edge deletion problems", IEEE Transactions on Circuits and Systems, 35 (3): 354–362, doi:10.1109/31.1748.
This article is issued from Wikipedia - version of the 6/26/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.