Drop impact
Drop impact occurs when a liquid drop strikes a solid or liquid surface. The resulting outcome depends on the properties of the drop, the surface, and the surrounding fluid, which is most commonly a gas.
Drop impact on a dry solid surface
When a liquid drop impacts a dry solid surface, it generally spreads on the surface, and then will retract if the impact is energetic enough to cause the drop to spread out more that it would generally spread due to its static receding contact angle. The specific outcome of the impact depends mostly upon the drop size, velocity, surface tension, viscosity, and also upon the surface roughness and the contact angle between the drop and the surface.[1]
Summary of possible drop impact outcomes
- "Deposition" is said to occur when the drop spreads on the surface at impact and remains attached to the surface during the entire impact process without breaking up.[1] This outcome is representative of impact of small, low-velocity drops onto smooth wetting surfaces.
- The "prompt splash" outcome occurs when the drop impacts a rough surface, and is characterized by the generation of droplets at the contact line (where solid, gas, and liquid meet) at the beginning of the process of spreading of the drop on the surface, when the liquid has a high outward velocity.[1]
- At reduced surface tension, the liquid layer can detach from the wall, resulting in a "corona splash".[2]

- On a wetting surface, "receding breakup" can occur as the liquid retracts from its maximum spreading radius, due to the fact that the contact angle decreases during retraction, causing some drops to be left behind by the receding drop.[1] On superhydrophobic surfaces, the retracting drop can break up into a number of fingers which are each capable of further breakup, likely due to capillary instability.[2] Such satellite droplets have been observed to break off from the impacting drop both during the spreading and retracting phases.[3]
- "Rebound" and "partial rebound" outcomes can occur when a drop recedes after impact. As the drop recedes to the impact point, the kinetic energy of the collapsing drop causes the liquid to squeeze upward, forming a vertical liquid column. The case where drop stays partially on the surface but launches one or more drops at its top is known as partial rebound, whereas the case where the entire drop leaves the solid surface due to this upward motion is known as complete rebound.[2] The difference between rebound and partial rebound is caused by the receding contact angle of the drop on the surface. For low values a partial rebound occurs, while for high values a complete rebound occurs (assuming that the drop recedes with enough kinetic energy).[1]
Drop impact on superhydrophobic surfaces
Small drop deformation
On superhydrophobic surfaces, liquid drops are observed to bounce off of the solid surface. Richard and Quéré showed that a small liquid drop was able to bounce off of a solid surface over 20 times before coming to rest.[4] Of particular interest is the length of time that the drop remains in contact with the solid surface. This is important in applications such as heat transfer and aircraft icing. To find a relationship between drop size and contact time for low Weber number impacts (We << 1) on superhydrophobic surfaces (which experience little deformation), a simple balance between inertia (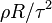 ) and capillarity (
) and capillarity (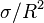 ) can be used,[5] as follows:
) can be used,[5] as follows:
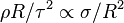
where 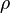 is the drop density, R is the drop radius,
is the drop density, R is the drop radius, 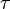 is the characteristic time scale, and
is the characteristic time scale, and 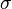 is the drop surface tension.
is the drop surface tension.
This yields
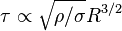 .
.
The contact time is independent of velocity in this regime. The minimum contact time for a low deformation drop (We << 1) is approximated by the lowest-order oscillation period for a spherical drop.,[6] giving the characteristic time a prefactor of approximately 2.2.[7] For large-deformation drops (We > 1), similar contact times are seen even though dynamics of impact are different, as discussed below.[7] If the droplet is split into multiple droplets, the contact time is reduced.[7]
By creating tapered surfaces with large spacing, the impacting droplet will exhibit the counterintuitive pancake bouncing, characterized by the droplet bouncing off at the end of spreading without retraction, resulting in ~80% contact time reduction.[8]
Significant drop deformation
As the Weber number increases, the drop deformation upon impact also increases. The drop deformation pattern can be split up into regimes based on the Weber number.[5]
- At We << 1, there is not significant deformation.
- For We on the order of 1, the drop experiences significant deformation, and flattens somewhat on the surface.
- When We ~ 4, waves form on the drop.
- When We ~ 18, satellite droplet(s) break off of the drop, which is now an elongated vertical column.
- For large We (for which the magnitude depends on the specific surface structure), many satellite drops break off during spreading and/or retraction of the drop.[3]
Drop impact on a wet solid surface
When a liquid drop impacts a wet solid surface (a surface covered with a thin layer of liquid that exceeds the height of surface roughness), either spreading or splashing will occur.[2] If the velocity is below a critical value, the liquid will spread on the surface, similar to deposition described above. If the velocity exceeds the critical velocity, splashing will occur. Splashing on thin fluid films occurs in the form of a corona, similar to that seen for dry solid surfaces. Under proper conditions, droplet hitting on a liquid interface can also display a superhydrophobic-like bouncing, characterized by the contact time, spreading dynamics and restitution coefficient independent of the underlying liquid properties.[9]
Drop impact on a liquid surface

When a liquid drop impacts the surface of a liquid reservoir, it will either float, bounce, coalesce with the liquid reservoir, or splash.[10] In the case of floating, a drop will float on the surface for several seconds. Cleanliness of the liquid surface is reportedly very important in the ability of drops to float.[11] Drop bouncing can occur on perturbed liquid surfaces.[10] If the drop is able to rupture a thin film of gas separating it from the liquid reservoir, it can coalesce. Finally, higher Weber number drop impacts (with greater energy) produce splashing. In the splashing regime, the impacting drop creates a crater in the fluid surface, followed by a crown around the crater. Additionally, a central jet, called the "Rayleigh jet," or "Worthington jet" protrudes from the center of the crater.[10] If the impact energy is high enough, the jet rises to the point where it pinches off, sending one or more droplets upward out of the surface.
See also
References
- 1 2 3 4 5 Rioboo, Romain, Cameron Tropea, and Marco Marengo. "Outcomes from a drop impact on solid surfaces." Atomization and Sprays 11.2 (2001)
- 1 2 3 4 Yarin, A. L. "Drop impact dynamics: splashing, spreading, receding, bouncing…." Annu. Rev. Fluid Mech. 38 (2006): 159-192
- 1 2 Tsai, Peichun, et al. "Drop impact upon micro-and nanostructured superhydrophobic surfaces." Langmuir 25.20 (2009): 12293-12298
- ↑ Richard, D., and D. Quéré. "Bouncing water drops." EPL (Europhysics Letters)50.6 (2000): 769
- 1 2 Richard, Denis, Christophe Clanet, and David Quéré. "Surface phenomena: Contact time of a bouncing drop." Nature 417.6891 (2002): 811-811
- ↑ Rayleigh, Lord. "On the capillary phenomena of jets." Proceedings of the Royal Society of London 29.196-199 (1879): 71-97
- 1 2 3 Bird, James C., et al. "Reducing the contact time of a bouncing drop." Nature 503.7476 (2013): 385-388
- ↑ Yahua Liu, Lisa Moevius, Xinpeng Xu,Tiezheng Qian, Julia M Yeomans, Zuankai Wang. "Pancake bouncing on superhydrophobic surfaces." Nature Physics, 10, 515-519 (2014)
- ↑ Chonglei Hao,Jing Li, Yuan Liu, Xiaofeng Zhou, Yahua Liu, Rong Liu, Lufeng Che, Wenzhong Zhou, Dong Sun, Lawrence Li, Lei Xu, Zuankai Wang. "Superhydrophobic-like tunable droplet bouncing on slippery liquid interfaces." Nature Communications, DOI: 10.1038/ncomms8986
- 1 2 3 Rein, Martin. "Phenomena of liquid drop impact on solid and liquid surfaces." Fluid Dynamics Research 12.2 (1993): 61-93
- ↑ Reynolds, Osborne. "On the floating of drops on the surface of water depending only on the purity of the surface." Proc. Manchester Lit. Phil. Soc 21.1 (1881)