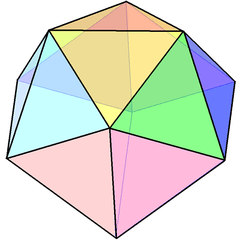
Edge-contracted icosahedron
| Edge-contracted icosahedron | |
|---|---|
 | |
| Faces | 18 triangles |
| Edges | 27 |
| Vertices | 11 |
| Symmetry | C2v, [2], (*22), order 4 |
| Vertex configuration | 2 (34) 8 (35) 1 (36) |
| Properties | Convex, deltahedron |
| Net | 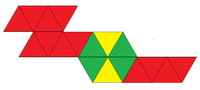 |
In geometry, an edge-contracted icosahedron is a polyhedron with 18 triangular faces, 27 edges, and 11 vertices with C2v symmetry, order 4.
Construction
It can be constructed from the regular icosahedron, with one edge contraction, removing one vertex, 3 edges, and 2 faces. This contraction distorts the circumscribed sphere original vertices. With all equilateral triangle faces, it has 2 sets of 3 coplanar equilateral triangles (each forming a half-hexagon), and thus is not a Johnson solid.
If the sets of coplanar triangles are considered a single face (called a triamond[1]), it has 10 vertices, 22 edges, and 14 faces, 12 triangles ![]() and 2 triamonds
and 2 triamonds ![]() .
.
It may also be described as having a hybrid square-pentagonal antiprismatic core (an antiprismatic core with one square base and one pentagonal base); each base is then augmented with a pyramid.
Related polytopes
The dissected regular icosahedron is a name for this polytope with the two sets of 3 coplanar faces as trapezoids. This is the vertex figure of a 4D polytope, grand antiprism. It has 10 vertices, 23 edges, and 11 equilateral triangular faces and 2 trapezoid faces.[2]
In chemistry
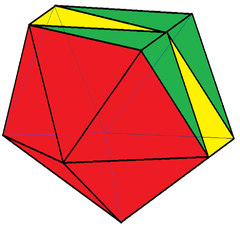
In chemistry, this polyhedron is most commonly called the octadecahedron, for 18 triangular faces, and represents the closo-boranate [B11H11]2−. [3]
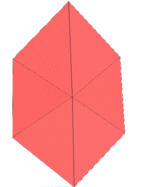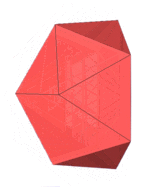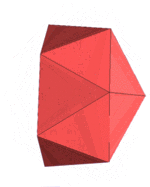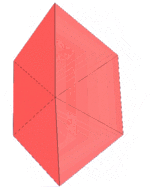 closo-boranate [B11H11]2− |
 Net |
Related polyhedra
The elongated octahedron is similar to the edge-contracted icosahedron, but instead of only one edge contracted, two opposite edges are contracted.
References
- ↑ http://www.interocitors.com/polyhedra/Triamonds/
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26) The Grand Antiprism
- ↑ Holleman, A. F.; Wiberg, E. (2001), Inorganic Chemistry, San Diego: Academic Press, p. 1165, ISBN 0-12-352651-5