Gibbs state

In probability theory and statistical mechanics, a Gibbs state is an equilibrium probability distribution which remains invariant under future evolution of the system. For example, a stationary or steady-state distribution of a Markov chain, such as that achieved by running a Markov chain Monte Carlo iteration for a sufficiently long time, is a Gibbs state.

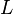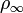Precisely, suppose $L \;$ is a generator of evolutions for an initial state $\rho_0 \;$, so that the state at any later time is given by $\rho(t) = e^{L t} [\rho_0] \;$. Then the condition for $\rho_{\infty} \;$ to be a Gibbs state is

$L [\rho_{\infty}] = 0$ .

In physics there may be several physically distinct Gibbs states in which a system may be trapped, particularly at lower temperatures.

They are named after Josiah Willard Gibbs, for his work in determining equilibrium properties of statistical ensembles. Gibbs himself referred to this type of statistical ensemble as being in "statistical equilibrium".^[1]

See also

• Gibbs algorithm
• Gibbs measure

References

1. ↑ Gibbs, Josiah Willard (1902). Elementary Principles in Statistical Mechanics, developed with especial reference to the rational foundation of thermodynamics. New York: Charles Scribner's Sons.