Glaeser's continuity theorem

In mathematical analysis, Glaeser's continuity theorem, is a characterization of the continuity of the derivative of the square roots of functions of class 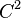$C^2$. It was introduced in 1963 by Georges Glaeser,^[1] and was later simplified by Jean Dieudonné.^[2]

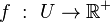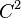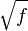The theorem states: Let $f\ :\ U \rightarrow \R^{+}$ be a function of class $C^{2}$ in an open set U contained in $\R^n$, then $\sqrt{f}$ is of class $C^{1}$ in U if and only if its partial derivatives of first and second order vanish in the zeros of f.

References

1. G. Glaeser, "Racine carrée d'une fonction différentiable", Annales de l'Institut Fourier 13, no 2 (1963), 203–210 : article
2. J. Dieudonné, "Sur un théorème de Glaeser", J. Analyse math. 23 (1970), 85–88 : Résumé Zbl, article p.85, article p.86, article p.87 (the p. 88, not shown on the free preview contains the reference to Glaeser)

External links

• Benjamin Hellouin. "Théorème de Glaeser" (in French)