Heart rate variability

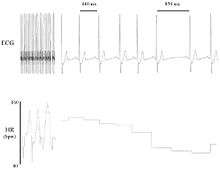
Electrocardiogram (ECG) recording of a canine heart that illustrates beat-to-beat variability in R–R interval (top) and heart rate (bottom).

Heart rate variability (HRV) is the physiological phenomenon of variation in the time interval between heartbeats. It is measured by the variation in the beat-to-beat interval.

Other terms used include: "cycle length variability", "RR variability" (where R is a point corresponding to the peak of the QRS complex of the ECG wave; and RR is the interval between successive Rs), and "heart period variability".

See also Heart rate turbulence, Sinus rhythm.

Methods used to detect beats include: ECG, blood pressure, ballistocardiograms,[1][2] and the pulse wave signal derived from a photoplethysmograph (PPG). ECG is considered superior because it provides a clear waveform, which makes it easier to exclude heartbeats not originating in the sinoatrial node. The term "NN" is used in place of RR to emphasize the fact that the processed beats are "normal" beats.

Clinical significance

Reduced HRV has been shown to be a predictor of mortality after myocardial infarction[3][4] although others have shown that the information in HRV relevant to acute myocardial infarction survival is fully contained in the mean heart rate.[5] A range of other outcomes/conditions may also be associated with modified (usually lower) HRV, including congestive heart failure, diabetic neuropathy, depression, post-cardiac transplant, susceptibility to SIDS and poor survival in premature babies.

Mental and social aspects

In the field of psychophysiology, there is interest in HRV. For example, HRV is related to emotional arousal. High-frequency (HF) activity has been found to decrease under conditions of acute time pressure and emotional strain[6] and elevated state anxiety,[7] presumably related to focused attention and motor inhibition.[7] HRV has been shown to be reduced in individuals reporting a greater frequency and duration of daily worry.[8] In individuals with post-traumatic stress disorder (PTSD), HRV and its HF component (see below) is reduced compared to controls whilst the low-frequency (LF) component is elevated. Furthermore, unlike controls, PTSD patients demonstrated no LF or HF reactivity to recalling a traumatic event.[9]

The Polyvagal Theory[10][11][12] derives from a psychophysiologic imputation of importance to HRV. This theory emphasizes the role of heart rate variability in understanding the magnitude and nature of vagal outflow to the heart. This theory decomposes heart rate variability based on frequency domain characteristics with an emphasis on respiratory sinus arrhythmia and its transmission by a neural pathway that is distinct from other components of HRV.[13] There is anatomic[14] and physiological[15] evidence for a polyvagal control of the heart.

Variation

Variation in the beat-to-beat interval is a physiological phenomenon. The SA node receives several different inputs and the instantaneous heart rate or RR interval and its variation are the results of these inputs.

The main inputs are the sympathetic and the parasympathetic nervous system (PSNS) and humoral factors. Respiration gives rise to waves in heart rate mediated primarily via the PSNS, and it is thought that the lag in the baroreceptor feedback loop may give rise to 10 second waves in heart rate (associated with Mayer waves of blood pressure), but this remains controversial.

Factors that affect the input are the baroreflex, thermoregulation, hormones, sleep-wake cycle, meals, physical activity, and stress.

Decreased PSNS activity or increased SNS activity will result in reduced HRV. High frequency (HF) activity (0.15 to 0.40 Hz), especially, has been linked to PSNS activity. Activity in this range is associated with the respiratory sinus arrhythmia (RSA), a vagally mediated modulation of heart rate such that it increases during inspiration and decreases during expiration. Less is known about the physiological inputs of the low frequency (LF) activity (0.04 to 0.15 Hz). Though previously thought to reflect SNS activity, it is now widely accepted that it reflects a mixture of both the SNS and PSNS.[16]

Heart rate variability phenomena

There are two primary fluctuations:

HRV artifact

Errors in the location of the instantaneous heart beat will result in errors in the calculation of the HRV. HRV is highly sensitive to artifact and errors in as low as even 2% of the data will result in unwanted biases in HRV calculations. To ensure accurate results therefore it is critical to manage artifact and R-R errors appropriately prior to performing any HRV analyses.[20][21]

Robust management of artifact, including RWave identification, interpolation and exclusion requires a high degree of care and precision. This can be very time consuming in large studies with data recorded over long durations. Powerful and specialized software packages, such as VivoSense, are available to assist users with a variety of robust and tested artifact management tools. These software programs also include some automated capability but it is important that a human review any automated artifact management and edit accordingly.

HRV analysis

The most widely used methods can be grouped under time-domain and frequency-domain. Other methods have been proposed, such as non-linear methods.

Time-domain methods

These are based on the beat-to-beat or NN intervals, which are analysed to give variables such as:

Geometric methods

The series of NN intervals also can be converted into a geometric pattern such as:

and so forth. A simple formula is then used that judges the variability on the basis of the geometric and/or graphics properties of the resulting pattern.

Frequency-domain methods

Frequency domain methods assign bands of frequency and then count the number of NN intervals that match each band. The bands are typically high frequency (HF) from 0.15 to 0.4 Hz, low frequency (LF) from 0.04 to 0.15 Hz, and the very low frequency (VLF) from 0.0033 to 0.04 Hz.

Several methods of analysis are available. Power spectral density (PSD), using parametric or nonparametric methods, provides basic information on the power distribution across frequencies. One of the most commonly used PSD methods is the discrete Fourier transform. Methods for the calculation of PSD may be generally classified as nonparametric and parametric. In most instances, both methods provide comparable results. The advantages of the nonparametric methods are (1) the simplicity of the algorithm used (fast Fourier transform [FFT] in most of the cases) and (2) the high processing speed. The advantages of parametric methods are (1) smoother spectral components that can be distinguished independent of preselected frequency bands, (2) easy postprocessing of the spectrum with an automatic calculation of low- and high-frequency power components with an easy identification of the central frequency of each component, and (3) an accurate estimation of PSD even on a small number of samples on which the signal is supposed to maintain stationarity. The basic disadvantage of parametric methods is the need of verification of the suitability of the chosen model and of its complexity (that is, the order of the model).

In addition to classical FFT-based methods used for the calculation of frequency parameters, a more appropriate PSD estimation method is the Lomb–Scargle (LS) periodogram.[26] Analysis has shown that the LS periodogram can produce a more accurate estimate of the PSD than FFT methods for typical RR data. Since the RR data is an unevenly sampled data, another advantage of the LS method is that in contrast to FFT-based methods it is able to be used without the need to resample and detrend the RR data.

A newly used HRV index, which depends on the wavelet entropy measures, is an alternative choice. The wavelet entropy measures are calculated using a three-step procedure defined in the literature. First, the wavelet packet algorithm is implemented using the Daubechies 4 (DB4) function as the mother wavelet with a scale of 7. Once the wavelet coefficients are obtained, the energy for each coefficient are calculated as described in the literature. After calculating the normalized values of wavelet energies, which represent the relative wavelet energy (or the probability distribution), the wavelet entropies are obtained using the definition of entropy given by Shannon.

Non-linear methods

Given the complexity of the mechanisms regulating heart rate, it is reasonable to assume that applying HRV analysis based on methods of non-linear dynamics will yield valuable information. Although chaotic behavior has been assumed, more rigorous testing has shown that heart rate variability cannot be described as a low dimensional chaotic process.[27] However, application of chaotic globals to HRV has been shown to predict diabetes status.[28] The most commonly used non-linear method of analysing heart rate variability is the Poincaré plot. Each data point represents a pair of successive beats, the x-axis is the current RR interval, while the y-axis is the previous RR interval. HRV is quantified by fitting mathematically defined geometric shapes to the data.[29] Other methods used are the correlation dimension, nonlinear predictability,[27] pointwise correlation dimension,[30] detrended fluctuation analysis,[31][32] approximate entropy, sample entropy,[33] multiscale entropy analysis,[34] sample asymmetry[35] and memory length (based on inverse statistical analysis).[36][37]

Long term correlations

Sequences of RR intervals have been found to have long-term correlations.[38][39] However, one flaw with these analyses is their lack of goodness-of-fit statistics, i.e. values are derived that may or may not have adequate statistical rigor. Different types of correlations have been found during different sleep stages.[40][39]

HRV analysis software

Duration and circumstances of ECG recording

Time domain methods are preferred to frequency domain methods when short-term recordings are investigated. This is due to the fact that the recording should be at least 10 times the wavelength of the lowest frequency bound of interest. Thus, recording of approximately 1 minute is needed to assess the HF components of HRV (i.e., a lowest bound of 0.15 Hz is a cycle of 6.6 seconds and so 10 cycles require ~60 seconds), while more than 4 minutes are needed to address the LF component (with a lower bound of 0.04 Hz).

Although time domain methods, especially the SDNN and RMSSD methods, can be used to investigate recordings of long durations, a substantial part of the long-term variability is day–night differences. Thus, long-term recordings analyzed by time domain methods should contain at least 18 hours of analyzable ECG data that include the whole night.

Physiological correlates of HRV components

Autonomic influences of heart rate

Although cardiac automaticity is intrinsic to various pacemaker tissues, heart rate and rhythm are largely under the control of the autonomic nervous system. The parasympathetic influence on heart rate is mediated via release of acetylcholine by the vagus nerve. Muscarinic acetylcholine receptors respond to this release mostly by an increase in cell membrane K+ conductance. Acetylcholine also inhibits the hyperpolarization-activated "pacemaker" current. The "Ik decay" hypothesis proposes that pacemaker depolarization results from slow deactivation of the delayed rectifier current, Ik, which, due to a time-independent background inward current, causes diastolic depolarization. Conversely, the "If activation" hypothesis suggests that after action potential termination, If provides a slowly activating inward current predominating over decaying Ik, thus initiating slow diastolic depolarization.

The sympathetic influence on heart rate is mediated by release of epinephrine and norepinephrine. Activation of β-adrenergic receptors results in cAMP-mediated phosphorylation of membrane proteins and increases in ICaL and in If the end result is an acceleration of the slow diastolic depolarization.

Under resting conditions, vagal tone prevails and variations in heart period are largely dependent on vagal modulation. The vagal and sympathetic activity constantly interact. Because the sinus node is rich in acetylcholinesterase, the effect of any vagal impulse is brief because the acetylcholine is rapidly hydrolyzed. Parasympathetic influences exceed sympathetic effects probably through two independent mechanisms: (1) a cholinergically induced reduction of norepinephrine released in response to sympathetic activity and (2) a cholinergic attenuation of the response to an adrenergic stimulus.

Components of HRV

The RR interval variations present during resting conditions represent beat-by-beat variations in cardiac autonomic inputs. However, efferent vagal (parasympathetic) activity is a major contributor to the HF component, as seen in clinical and experimental observations of autonomic maneuvers such as electrical vagal stimulation, muscarinic receptor blockade, and vagotomy. More problematic is the interpretation of the LF component, which was considered by some as a marker of sympathetic modulation (especially when expressed in normalized units) but is now known to include both sympathetic and vagal influences. For example, during sympathetic activation the resulting tachycardia is usually accompanied by a marked reduction in total power, whereas the reverse occurs during vagal activation. Thus the spectral components change in the same direction and do not indicate that LF faithfully reflects sympathetic effects.

It is important to note that HRV measures fluctuations in autonomic inputs to the heart rather than the mean level of autonomic inputs. Thus, both withdrawal and saturatingly high levels of autonomic input to the heart can lead to diminished HRV.

Changes of HRV related to specific pathologies

A reduction of HRV has been reported in several cardiovascular and noncardiovascular diseases.

Myocardial infarction

Depressed HRV after MI may reflect a decrease in vagal activity directed to the heart. HRV in patients surviving an acute MI reveal a reduction in total and in the individual power of spectral components. The presence of an alteration in neural control is also reflected in a blunting of day-night variations of RR interval. In post-MI patients with a very depressed HRV, most of the residual energy is distributed in the VLF frequency range below 0.03 Hz, with only a small respiration-related variations.

Diabetic neuropathy

In neuropathy associated with diabetes mellitus characterized by alteration in small nerve fibers, a reduction in time domain parameters of HRV seems not only to carry negative prognostic value but also to precede the clinical expression of autonomic neuropathy. In diabetic patients without evidence of autonomic neuropathy, reduction of the absolute power of LF and HF during controlled conditions was also reported. Similarly, diabetic patients can be differentiated from normal controls on the basis of reduction in HRV.[28]

Cardiac transplantation

A very reduced HRV with no definite spectral components has been reported in patients with a recent heart transplant. The appearance of discrete spectral components in a few patients is considered to reflect cardiac reinnervation. This reinnervation may occur as early as 1 to 2 years after transplantation and is assumed to be of sympathetic origin. In addition, a correlation between respiratory rate and the HF component of HRV observed in some transplanted patients also indicates that a nonneural mechanism may generate a respiration-related rhythmic oscillation.

Myocardial dysfunction

A reduced HRV has been observed consistently in patients with cardiac failure. In this condition characterized by signs of sympathetic activation such as faster heart rates and high levels of circulating catecholamines, a relation between changes in HRV and the extent of left ventricular dysfunction was reported. In fact, whereas the reduction in time domain measures of HRV seemed to parallel the severity of the disease, the relationship between spectral components and indices of ventricular dysfunction appears to be more complex. In particular, in most patients with a very advanced phase of the disease and with a drastic reduction in HRV, an LF component could not be detected despite the clinical signs of sympathetic activation. This reflects that, as stated above, the LF may not accurately reflect cardiac sympathetic tone.

Liver cirrhosis

Liver cirrhosis is associated with decreased HRV. Decreased HRV in patients with cirrhosis has a prognostic value and predicts mortality. Loss of HRV is also associated with higher plasma pro-inflammatory cytokine levels and impaired neurocognitive function in this patient population.[41]

Sepsis

HRV is decreased in patients with sepsis. Loss of HRV has both diagnostic and prognostic value in neonates with sepsis.[42] The pathophysiology of decreased HRV in sepsis is not well understood but there is experimental evidence to show that partial uncoupling of cardiac pacemaker cells from autonomic neural control may play a role in decreased HRV during acute systemic inflammation.[43]

Tetraplegia

Patients with chronic complete high cervical spinal cord lesions have intact efferent vagal neural pathways directed to the sinus node. However, an LF component can be detected in HRV and arterial pressure variabilities of some tetraplegic patients. Thus, the LF component of HRV in those without intact sympathetic inputs to the heart represent vagal modulation.

Modifications of HRV by specific interventions

Interventions that augment HRV may be protective against cardiac mortality and sudden cardiac death. Although the rationale for changing HRV is sound, it also contains the inherent danger of leading to the unwarranted assumption that modification of HRV translates directly into cardiac protection, which may not be the case. Despite the growing consensus that increases in vagal activity can be beneficial, it is not as yet known how much vagal activity (or HRV as a marker) has to increase in order to provide adequate protection.

β-Adrenergic blockade and HRV

The data on the effect of β-blockers on HRV in post-MI patients are surprisingly scant. Despite the observation of statistically significant increases, the actual changes are very modest. In conscious post-MI dogs, β-blockers do not modify HRV. The unexpected observation that before MI, β-blockade increases HRV only in the animals destined to be at low risk for lethal arrhythmias after MI may suggest novel approaches to post-MI risk stratification.

Antiarrhythmic drugs and HRV

Data exist for several antiarrhythmic drugs. Flecainide and propafenone but not amiodarone were reported to decrease time domain measures of HRV in patients with chronic ventricular arrhythmia. In another study, propafenone reduced HRV and decreased LF much more than HF. A larger study confirmed that flecainide, also encainide and moricizine, decreased HRV in post-MI patients but found no correlation between the change in HRV and mortality during follow-up. Thus, some antiarrhythmic drugs associated with increased mortality can reduce HRV. However, it is not known whether these changes in HRV have any direct prognostic significance.

Scopolamine and HRV

Low-dose muscarinic receptor blockers, such as atropine and scopolamine, may produce a paradoxical increase in vagal effects on the heart, as suggested by a decrease in heart rate. In addition, scopolamine and low dose atropine can markedly increase HRV. However, though the heart rate slowing in proportional to the (low) does of atropine, the increase in HRV varies widely across and within individuals. This suggests that even for vagal activity to the heart, HRV may be a limited marker.

Thrombolysis and HRV

The effect of thrombolysis on HRV (assessed by pNN50) was reported in 95 patients with acute MI. HRV was higher 90 minutes after thrombolysis in the patients with patency of the infarct-related artery. However, this difference was no longer evident when the entire 24 hours were analyzed.

Exercise training and HRV

Exercise training may decrease cardiovascular mortality and sudden cardiac death. Regular exercise training is also thought to modify cardiac autonomic control. Individuals who exercise regularly have a 'training bradycardia' (i.e., low resting heart rate) and generally have higher HRV than sedentary individuals.

Biofeedback

Graph shows same person, actual readings. First half in stress, second in focus,relax situation. Recorded by Stone Biofeedback device.

The technique called resonant breathing biofeedback teaches how to recognize and control involuntary heart rate variability. A randomized study by Sutarto et al. assessed the effect of resonant breathing biofeedback among manufacturing operators; depression, anxiety and stress significantly decreased.[44]

Wind Instruments

One study that surveyed the physiological effects of playing Native American flutes found a significant HRV increase when playing both low-pitched and high-pitched flutes.[45]

Normal values of standard measures of HRV

Even though that there are no widely accepted standard values for HRV that can be used for clinical purposes, The Task Force of the European Society of Cardiology and Heart Rhythm Society (formerly called North American Society of Pacing Electrophysiology) provided initial normative values of standard measures of HRV[46]

Example reading from an HRV app
Example live reading from an HRV app - showing rise and fall of heart rate and breathing pacer


Sources

  1. ↑ Brüser, Christoph; Stadlthanner, Kurt; de Waele, Stijn; Leonhardt, Steffen (2011). "Adaptive Beat-to-Beat Heart Rate Estimation in Ballistocardiograms". IEEE Transactions on Information Technology in Biomedicine. IEEE. 15 (5): 778–786. doi:10.1109/TITB.2011.2128337. PMID 21421447.
  2. ↑ Brüser, Christoph; Winter, Stefan; Leonhardt, Steffen (2012). "Unsupervised Heart Rate Variability Estimation from Ballistocardiograms". 7th International Workshop on Biosignal Interpretation (BSI 2012), Como, Italy.
  3. ↑ Bigger JT Jr; Fleiss JL; Steinman RC; Rolnitzky LM; Kleiger RE; Rottman JN. (1992). "Frequency domain measures of heart period variability and mortality after myocardial infarction". Circulation. 85 (1): 164–171. doi:10.1161/01.CIR.85.1.164. PMID 1728446.
  4. ↑ Kleiger RE, Miller JP, Bigger JT Jr, Moss AJ (1987). "Decreased heart rate variability and its association with increased mortality after acute myocardial infarction". Am J Cardiol. 59 (4): 256–262. doi:10.1016/0002-9149(87)90795-8. PMID 3812275.
  5. ↑ Abildstrom SZ, Jensen BT, Agner E, et al. (2003). "Heart rate versus heart rate variability in risk prediction after myocardial infarction". Journal of Cardiovascular Electrophysiology. 14 (2): 168–73. doi:10.1046/j.1540-8167.2003.02367.x. PMID 12693499.
  6. ↑ Nickel, P.; F. Nachreiner (2003). "Sensitivity and Diagnostics of the 0.1-Hz Component of Heart Rate Variability as an Indicator of Mental Workload". Human Factors. 45 (4): 575–590. doi:10.1518/hfes.45.4.575.27094. PMID 15055455.
  7. 1 2 Jönsson, P. (2007). "Respiratory sinus arrhythmia as a function of state anxiety in healthy individuals". International Journal of Psycho-physiology. 63 (1): 48–54. doi:10.1016/j.ijpsycho.2006.08.002. PMID 16989914.
  8. ↑ Brosschot, J.F.; E. Van Dijk; J.F. Thayer (2007). "Daily worry is related to low heart rate variability during waking and the subsequent nocturnal sleep period". International Journal of Psychophysiology. 63 (1): 39–47. doi:10.1016/j.ijpsycho.2006.07.016. PMID 17020787.
  9. ↑ Hagit, C.; et al. (1998). "Analysis of heart rate variability in posttraumatic stress disorder patients in response to a trauma-related reminder". Biological Psychiatry. 44 (10): 1054–1059. doi:10.1016/S0006-3223(97)00475-7. PMID 9821570.
  10. ↑ PORGES, S. W. (1 April 2009). "The polyvagal theory: New insights into adaptive reactions of the autonomic nervous system". Cleveland Clinic Journal of Medicine. 76 (Suppl_2): S86–S90. doi:10.3949/ccjm.76.s2.17. PMC 3108032Freely accessible. PMID 19376991.
  11. ↑ Porges, SW (August 2003). "The Polyvagal Theory: phylogenetic contributions to social behavior". Physiology & Behavior. 79 (3): 503–13. doi:10.1016/S0031-9384(03)00156-2. PMID 12954445.
  12. ↑ Porges, Stephen W. The polyvagal theory : neurophysiological foundations of emotions, attachment, communication, and self-regulation (1st ed.). New York: W. W. Norton. ISBN 0393707008.
  13. ↑ Porges, Stephen W. (February 2007). "The polyvagal perspective". Biological Psychology. 74 (2): 116–143. doi:10.1016/j.biopsycho.2006.06.009. PMC 1868418Freely accessible. PMID 17049418.
  14. ↑ Haselton, JR; Solomon, IC; Motekaitis, AM; Kaufman, MP (September 1992). "Bronchomotor vagal preganglionic cell bodies in the dog: an anatomic and functional study". Journal of applied physiology (Bethesda, Md. : 1985). 73 (3): 1122–9. PMID 1400025.
  15. ↑ Gatti PJ, Johnson TA, Massari VJ (February 1996). "Can neurons in the nucleus ambiguus selectively regulate cardiac rate and atrio-ventricular conduction?". Journal of the Autonomic Nervous System. 57 (1–2): 123–127. doi:10.1016/0165-1838(95)00104-2. PMID 8867095.
  16. ↑ Billman, George E. (2013). "The LF/HF ratio does not accurately measure cardiac sympatho-vagal balance". Frontiers in Physiology. 4: 26. doi:10.3389/fphys.2013.00026. PMC 3576706Freely accessible. PMID 23431279.
  17. ↑ Hales S. Statistical Essays: Containing Haemastaticks. London, UK: Innys, Manby and Woodward; 1733.
  18. ↑ von Haller A. Elementa Physiologica. Lausanne, Switzerland: 1760; T II, Lit VI, 330
  19. ↑ Sayers (1973). "Analysis of Heart Rate Variability". Ergonomics. 16 (1): 17–32. doi:10.1080/00140137308924479. PMID 4702060.
  20. ↑ Citi, L.; Brown, E.N.; Barbieri, R. (2012). "Online tool for the detection and correction of erroneous and ectopic heartbeats".
  21. ↑ Citi, L.; Brown, E.N.; Barbieri, R. (2012). "A real-time automated point-process method for the detection and correction of erroneous and ectopic heartbeats". IEEE Trans Biomed Eng. 59: 2828–2837. doi:10.1109/TBME.2012.2211356.
  22. ↑ Mietus, J E; Peng, C.K.; Henry, I.; Goldsmith, R.L.; Goldberger, A.L. (2002). "The pNNx files: re–examining a widely used heart rate variability measure". Heart. 88: 378–380. doi:10.1136/heart.88.4.378.
  23. ↑ Clinton F. Goss; Eric B. Miller (August 2013). "Dynamic Metrics of Heart Rate Variability". arXiv:1308.6018Freely accessible.
  24. ↑ Parameter aus dem Lorenz-Plot (Parameters from the Lorenz-Plot brain & heart, "Parameter der Herzratenvariabilität" (Parameters of HRV), by Dr. Egon Winter, Austria. Accessed 2016-11-20. In German.
  25. ↑ 'LORENZ CURVE' command in online user manual for 'Dataplot' software, published by NIST, U.S.A. Accessed via Version cached by Google on 2016-10-28 on 2016-11-20.
  26. ↑ Isler, Yalcin; Kuntalp, M. (2007). "Combining classical HRV indices with wavelet entropy measures improves to performance in diagnosing congestive heart failure". Computers in Biology and Medicine. 37 (10): 1502–1510. doi:10.1016/j.compbiomed.2007.01.012.
  27. 1 2 Kanters JK, Holstein-Rathlou NH, Agner E (1994). "Lack of evidence for low-dimensional chaos in heart rate variability". Journal of Cardiovascular Electrophysiology. 5 (7): 591–601. doi:10.1111/j.1540-8167.1994.tb01300.x. PMID 7987529.
  28. 1 2 De Souza, Naiara Maria; Vanderlei, Luiz Carlos M.; Garner, David M. (2 January 2015). "Risk evaluation of diabetes mellitus by relation of chaotic globals to HRV". Complexity. 20 (3): 84–92. doi:10.1002/cplx.21508.
  29. ↑ Brennan M,Palaniswami M, Kamen P. Do existing measures of Poincaré plot geometry reflect non-linear features of heart rate variability? Biomedical Engineering, IEEE Transactions on, Proc. IEEE Transactions on Biomedical Engineering, 2001, 48, 1342-1347
  30. ↑ Storella, Robert J.; Wood, Harrison W.; Mills, Kenneth M.; Kanters, Jørgen K.; Højgaard, Michael V.; Holstein-Rathlou, Niels-Henrik (October 1998). "Approximate entropy and point correlation dimension of heart rate variability in healthy subjects". Integrative Physiological and Behavioral Science. 33 (4): 315–320. doi:10.1007/BF02688699.
  31. ↑ Kantelhardt, Jan W; Koscielny-Bunde, Eva; Rego, Henio H.A; Havlin, Shlomo; Bunde, Armin (2001). "Detecting long-range correlations with detrended fluctuation analysis". Physica A: Statistical Mechanics and its Applications. 295 (3-4): 441–454. doi:10.1016/S0378-4371(01)00144-3. ISSN 0378-4371.
  32. ↑ Peng, C.-K.; Havlin, Shlomo; Stanley, H. Eugene; Goldberger, Ary L. (1995). "Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series". Chaos: An Interdisciplinary Journal of Nonlinear Science. 5 (1): 82. doi:10.1063/1.166141. ISSN 1054-1500.
  33. ↑ Richman, JS; Moorman, JR (June 2000). "Physiological time-series analysis using approximate entropy and sample entropy.". American Journal of Physiology. Heart and Circulatory Physiology. 278 (6): H2039–49. PMID 10843903.
  34. ↑ Costa, M; Goldberger, AL; Peng, CK (5 August 2002). "Multiscale entropy analysis of complex physiologic time series.". Physical Review Letters. 89 (6): 068102. doi:10.1103/physrevlett.89.068102. PMID 12190613.
  35. ↑ Kovatchev, BP; Farhy, LS; Cao, H; Griffin, MP; Lake, DE; Moorman, JR (December 2003). "Sample asymmetry analysis of heart rate characteristics with application to neonatal sepsis and systemic inflammatory response syndrome.". Pediatric research. 54 (6): 892–8. doi:10.1203/01.pdr.0000088074.97781.4f. PMID 12930915.
  36. ↑ Shirazi, AH; Raoufy, MR; Ebadi, H; De Rui, M; Schiff, S; Mazloom, R; Hajizadeh, S; Gharibzadeh, S; Dehpour, AR; Amodio, P; Jafari, GR; Montagnese, S; Mani, AR (2013). "Quantifying memory in complex physiological time-series.". PLOS ONE. 8 (9): e72854. doi:10.1371/journal.pone.0072854. PMC 3764113Freely accessible. PMID 24039811.
  37. ↑ Ebadi, H; Shirazi, A H; Mani, Ali R; Jafari, G R (24 August 2011). "Inverse statistical approach in heartbeat time series". Journal of Statistical Mechanics: Theory and Experiment. 2011 (08): P08014. doi:10.1088/1742-5468/2011/08/P08014.
  38. ↑ C.-K. Peng, J. Mietus, J. M. Hausdorff, S. Havlin, H. E. Stanley, A. L. Goldberger; Mietus, J.; Hausdorff, J.; Havlin, S.; Stanley, H.; Goldberger, A. (1993). "Long-range anticorrelations and non-gaussian behavior of the heartbeat". Phys. Rev. Lett. 70 (9): 1343–6. doi:10.1103/PhysRevLett.70.1343. PMID 10054352.
  39. 1 2 Bailly, Francis; Longo, Giuseppe; Montevil, Mael (2011-09-01). "A 2-dimensional geometry for biological time". Progress in Biophysics and Molecular Biology. 106 (3): 474–484. doi:10.1016/j.pbiomolbio.2011.02.001.
  40. ↑ Bunde, Armin; Havlin, Shlomo; Kantelhardt, Jan W.; Penzel, Thomas; Peter, Jörg-Hermann; Voigt, Karlheinz (2000). "Correlated and Uncorrelated Regions in Heart-Rate Fluctuations during Sleep". Physical Review Letters. 85 (17): 3736–3739. Bibcode:2000PhRvL..85.3736B. doi:10.1103/PhysRevLett.85.3736. ISSN 0031-9007.
  41. ↑ Mani, AR; Montagnese, S; Jackson, CD; Jenkins, CW; Head, IM; Stephens, RC; Moore, KP; Morgan, MY (February 2009). "Decreased heart rate variability in patients with cirrhosis relates to the presence and degree of hepatic encephalopathy.". American Journal of Physiology. Gastrointestinal and Liver Physiology. 296 (2): G330–8. doi:10.1152/ajpgi.90488.2008. PMID 19023029.
  42. ↑ Griffin, MP; Moorman, JR (January 2001). "Toward the early diagnosis of neonatal sepsis and sepsis-like illness using novel heart rate analysis.". Pediatrics. 107 (1): 97–104. doi:10.1542/peds.107.1.97. PMID 11134441.
  43. ↑ Gholami, M; Mazaheri, P; Mohamadi, A; Dehpour, T; Safari, F; Hajizadeh, S; Moore, KP; Mani, AR (February 2012). "Endotoxemia is associated with partial uncoupling of cardiac pacemaker from cholinergic neural control in rats.". Shock (Augusta, Ga.). 37 (2): 219–27. doi:10.1097/shk.0b013e318240b4be. PMID 22249221.
  44. ↑ Sutarto, AP; Wahab, MN; Zin NM (2012). "Resonant breathing biofeedback training for stress reduction among manufacturing operators". Int J Occup Saf Ergon. 18 (4): 549–61. PMID 23294659.
  45. ↑ Eric B. Miller; Clinton F. Goss (January 2014). "An Exploration of Physiological Responses to the Native American Flute" (PDF). arXiv:1401.6004Freely accessible. Retrieved 25 Jan 2014.
  46. ↑ Camm; et al. (1996). "Heart Rate Variability: Standards of Measurement,Physiological Interpretation, and Clinical use". Circulation. 93: 1043–1065. doi:10.1161/01.cir.93.5.1043.

External links

This article is issued from Wikipedia - version of the 12/4/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.