Hyperstability
In stability theory, hyperstability is a property of a system that requires the state vector to remain bounded if the inputs are restricted to belonging to a subset of the set of all possible inputs.[1]
Definition:[2] A system is hyperstable if there are two constants 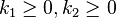 such that any state trajectory of the system satisfies the inequality:
such that any state trajectory of the system satisfies the inequality:
References
- ↑ Brian D. O Anderson, "A Simplified Viewpoint of Hyperstability", IEEE Transactions on Automatic Control, June 1968
- ↑ Zinober, Deterministic control of uncertain systems, 1990
See also
This article is issued from Wikipedia - version of the 3/1/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.