Invertible module
In mathematics, particularly commutative algebra, an invertible module is intuitively a module that has an inverse with respect to the tensor product. Invertible modules form the foundation for the definition of invertible sheaves in algebraic geometry.
Formally, a finitely generated module M over a ring R is said to be invertible if it is locally a free module of rank 1. In other words, 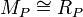 for all primes P of R. Now, if M is an invertible R-module, then its dual M* = Hom(M,R) is its inverse with respect to the tensor product, i.e.
for all primes P of R. Now, if M is an invertible R-module, then its dual M* = Hom(M,R) is its inverse with respect to the tensor product, i.e. 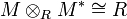 .
.
The theory of invertible modules is closely related to the theory of codimension one varieties including the theory of divisors.
See also
References
- Eisenbud, David, Commutative Algebra with a View Toward Algebraic Geometry, Springer, ISBN 978-0-387-94269-8
This article is issued from Wikipedia - version of the 1/18/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.