Irregularity of distributions

The irregularity of distributions problem, stated first by Hugo Steinhaus, is a numerical problem with a surprising result. The problem is to find N numbers, $x_1,\ldots,x_N$, all between 0 and 1, for which the following conditions hold:

• The first two numbers must be in different halves (one less than 1/2, one greater than 1/2).
• The first 3 numbers must be in different thirds (one less than 1/3, one between 1/3 and 2/3, one greater than 2/3).
• The first 4 numbers must be in different fourths.
• The first 5 numbers must be in different fifths.
• etc.

Mathematically, we are looking for a sequence of real numbers

$x_1,\ldots,x_N$

such that for every n ∈ {1, ..., N} and every k ∈ {1, ..., n} there is some i ∈ {1, ..., n} such that

${\displaystyle {\frac {k-1}{n}}\leq x_{i}<{\frac {k}{n}}.}$

Solution

The surprising result is that there is a solution up to N = 17, but starting at N = 18 and above it is impossible. A possible solution for N ≤ 17 is shown diagrammatically on the right; numerically it is as follows:

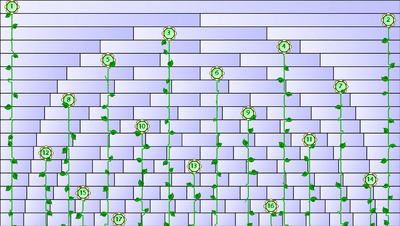
A possible solution for N = 17 shown diagrammatically. In each row n, there are n “vines” which are all in different n^ths. For example, looking at row 5, it can be seen that 0 < x₁ < 1/5 < x₅ < 2/5 < x₃ < 3/5 < x₄ < 4/5 < x₂ < 1. The numerical values are printed in the article text.

${\displaystyle {\begin{aligned}x_{1}&=0.029\\x_{2}&=0.971\\x_{3}&=0.423\\x_{4}&=0.71\\x_{5}&=0.27\\x_{6}&=0.542\\x_{7}&=0.852\\x_{8}&=0.172\\x_{9}&=0.62\\x_{10}&=0.355\\x_{11}&=0.774\\x_{12}&=0.114\\x_{13}&=0.485\\x_{14}&=0.926\\x_{15}&=0.207\\x_{16}&=0.677\\x_{17}&=0.297\end{aligned}}}$

In this example, considering for instance the first 5 numbers, we have

${\displaystyle 0<x_{1}<{\frac {1}{5}}<x_{5}<{\frac {2}{5}}<x_{3}<{\frac {3}{5}}<x_{4}<{\frac {4}{5}}<x_{2}<1.}$

References

• H. Steinhaus, One hundred problems in elementary mathematics, Basic Books, New York, 1964, page 12
• Berlekamp, E. R.; Graham, R. L. (1970). "Irregularities in the distributions of finite sequences". Journal of Number Theory. 2: 152–161. doi:10.1016/0022-314X(70)90015-6. MR 0269605.
• M. Warmus, "A Supplementary Note on the Irregularities of Distributions", Journal of Number Theory 8, 260–263, 1976.