Jenkins hash function

The Jenkins hash functions are a collection of (non-cryptographic) hash functions for multi-byte keys designed by Bob Jenkins. The first one was formally published in 1997.

The hash functions

one-at-a-time

Jenkins's one-at-a-time hash is adapted here from a WWW page by Bob Jenkins,^[1] which is an expanded version of his Dr. Dobbs article.^[2]

uint32_t jenkins_one_at_a_time_hash(const uint8_t* key, size_t length) {
  size_t i = 0;
  uint32_t hash = 0;
  while (i != length) {
    hash += key[i++];
    hash += hash << 10;
    hash ^= hash >> 6;
  }
  hash += hash << 3;
  hash ^= hash >> 11;
  hash += hash << 15;
  return hash;
}

Avalanche behavior of Jenkins One-at-a-time hash over 3-byte keys

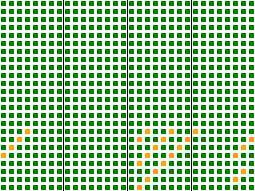
The avalanche behavior of this hash is shown on the right.

Each of the 24 rows corresponds to a single bit in the 3-byte input key, and each of the 32 columns corresponds to a bit in the output hash. Colors are chosen by how well the input key bit affects the given output hash bit: a green square indicates good mixing behavior, a yellow square weak mixing behavior, and red would indicate no mixing. Only a few bits in the last byte of the input key are weakly mixed to a minority of bits in the output hash.

The standard implementation of the Perl programming language includes Jenkins's one-at-a-time hash and SipHash, and uses Jenkins's one-at-a-time hash by default.^[3][4]

lookup2

The lookup2 function was an interim successor to one-at-a-time. It is the function referred to as "My Hash" in the 1997 Dr. Dobbs journal article, though it has been obsoleted by subsequent functions that Jenkins has released. Applications of this hash function are found in:

• the SPIN model checker, for probabilistic error detection. In a paper about this program, researchers Dillinger and Manolios note that lookup2 is "a popular choice among implementers of hash tables and Bloom filters". They study lookup2 and a simple extension of it that produces 96-bit rather than 32-bit hash values.^[5]
• The Netfilter firewall component of Linux,^[6] where it replaced an earlier hash function that was too sensitive to collisions. The resulting system, however, was shown to still be sensitive hash flooding attacks, even when the Jenkins hash is randomized using a secret key.^[7]
• The program that solved the game of kalah used the Jenkins hash function, instead of the Zobrist hashing technique more commonly used for this type of problem; the reasons for this choice were the speed of Jenkins' function on the small representations of kalah boards, as well as the fact that the basic rule of kalah can radically alter the board, negating the benefit of Zobrist's incremental computation of hash functions.^[8]

lookup3

The lookup3 function consumes input in 12 byte (96 bit) chunks.^[9] It may be appropriate when speed is more important than simplicity. Note, though, that any speed improvement from the use of this hash is only likely to be useful for large keys, and that the increased complexity may also have speed consequences such as preventing an optimizing compiler from inlining the hash function.

SpookyHash

In 2011 Jenkins released a new 128-bit hash function called SpookyHash.^[10] SpookyHash is significantly faster than lookup3.

See also

• CityHash
• Fowler Noll Vo hash
• MurmurHash

References

1. Jenkins, Bob (c. 2006). "A hash function for hash Table lookup". Retrieved April 16, 2009.
2. Jenkins, Bob (September 1997). "Hash functions". Dr. Dobbs Journal.
3. "RFC: perlfeaturedelta": "one-at-a-time hash algorithm ... [was added in version] 5.8.0"
4. "perl: hv_func.h"
5. Dillinger, Peter C.; Manolios, Panagiotis (2004). Fast and accurate bitstate verification for SPIN. Proc. 11th International SPIN Workshop. pp. 57–75. CiteSeerX 10.1.1.4.6765.
6. Neira Ayuso, Pablo (2006). "Netfilter's connection tracking system" (PDF). ;login:. 31 (3).
7. Bar-Yosef, Noa; Wool, Avishai (2007). Remote algorithmic complexity attacks against randomized hash tables Proc. International Conference on Security and Cryptography (SECRYPT) (PDF). pp. 117–124.
8. Irving, Geoffrey; Donkers, Jeroen; Uiterwijk, Jos. "Solving kalah" (PDF). ICGA Journal.
9. Jenkins, Bob. "lookup3.c source code". Retrieved April 16, 2009.
10. Jenkins, Bob. "SpookyHash: a 128-bit noncryptographic hash". Retrieved Jan 29, 2012.