K-homology
In mathematics, K-homology is a homology theory on the category of locally compact Hausdorff spaces. It classifies the elliptic pseudo-differential operators acting on the vector bundles over a space. In terms of 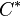 -algebras, it classifies the Fredholm modules over an algebra.
-algebras, it classifies the Fredholm modules over an algebra.
An operator homotopy between two Fredholm modules 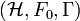 and
and 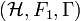 is a norm continuous path of Fredholm modules,
is a norm continuous path of Fredholm modules, 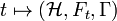 ,
, ![t \in [0,1].](../I/m/de4ef1e33d30a0fa6fc661f8fed20bde.png) Two Fredholm modules are then equivalent if they are related by unitary transformations or operator homotopies. The
Two Fredholm modules are then equivalent if they are related by unitary transformations or operator homotopies. The 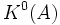 group is the abelian group of equivalence classes of even Fredholm modules over A. The
group is the abelian group of equivalence classes of even Fredholm modules over A. The 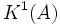 group is the abelian group of equivalence classes of odd Fredholm modules over A. Addition is given by direct summation of Fredholm modules, and the inverse of
group is the abelian group of equivalence classes of odd Fredholm modules over A. Addition is given by direct summation of Fredholm modules, and the inverse of 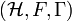 is
is 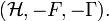
References
- N. Higson and J. Roe, Analytic K-homology. Oxford University Press, 2000.
This article incorporates material from K-homology on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.