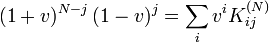Krawtchouk matrices
In mathematics, Krawtchouk matrices are matrices whose entries are values of Krawtchouk polynomials at nonnegative integer points.[1] [2] The Krawtchouk matrix K(N) is an (N+1)×(N+1) matrix. Here are the first few examples:
![K^{(0)}=\begin{bmatrix}
1
\end{bmatrix}
\qquad
K^{(1)}=\left [ \begin{array}{rr}
1&1\\
1&-1
\end{array}\right ]
\qquad
K^{(2)}=\left [ \begin{array}{rrr}
1&1&1\\
2&0&-2\\
1&-1&1
\end{array}\right ]
\qquad
K^{(3)}=\left [ \begin{array}{rrrr}
1&1&1&1\\
3&1&-1&-3\\
3&-1&-1&3\\
1&-1&1&-1
\end{array}\right ]](../I/m/4a6dec20e3877021e0cb2803eeb50418.png)
![K^{(4)}=\left [ \begin{array}{rrrrr}
1&1&1&1&1\\
4&2&0&-2&-4\\
6&0&-2&0&6\\
4&-2&0&2&-4\\
1&-1&1&-1&1
\end{array}\right ]
\qquad
K^{(5)}=\left [ \begin{array}{rrrrrr}
1& 1& 1& 1& 1& 1\\
5& 3& 1&-1&-3&-5\\
10& 2&-2&-2& 2& 10\\
10& -2&-2& 2& 2&-10\\
5& -3& 1& 1&-3&5\\
1& -1& 1&-1& 1&-1
\end{array}\right ].](../I/m/ebf47d91d069f537dcdaf6240a5a8579.png)
In general, for positive integer 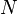 , the entries
, the entries 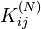 are given via the generating function
are given via the generating function
where the row and column indices 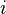 and
and 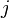 run from
run from  to
to 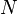 .
.
These Krawtchouk polynomials are orthogonal with respect to symmetric binomial distributions, 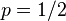 .[3]
.[3]
See also
References
- ↑ N. Bose, “Digital Filters: Theory and Applications” [North-Holland Elsevier, N.Y., 1985]
- ↑ P. Feinsilver, J. Kocik: Krawtchouk polynomials and Krawtchouk matrices, Recent advances in applied probability, Springer-Verlag, October, 2004
- ↑ Hahn Class: Definitions
External links
This article is issued from Wikipedia - version of the 4/6/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.