Laves phase

Unit cell of Laves phase with MgZn₂ structure (Mg atoms are green).

Laves polyhedron

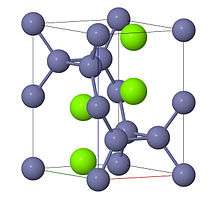
Laves phases are intermetallic phases that have composition AB₂ and are named for Fritz Laves who first described them. The phases are classified on the basis of geometry alone. There are three different classification classes: cubic MgCu₂ (C15), hexagonal MgZn₂ (C14), and hexagonal MgNi₂ (C36). The latter two classes are unique forms of the hexagonal arrangement, but share the same basic structure. In general, the A atoms are ordered as in diamond, hexagonal diamond, or a related structure, and the B atoms form tetrahedra around the A atoms for the AB₂ structure.^[1] Laves phases are of particular interest in modern metallurgy research because of their abnormal physical and chemical properties. Many hypothetical or primitive applications have been developed. However, little practical knowledge has been elucidated from Laves phase study so far. A characteristic feature is the almost perfect electrical conductivity, but they are not plastically deformable at room temperature.

In each of the three classes of Laves phase, if the two types of atom were perfect spheres with a size ratio of ${\displaystyle {\sqrt {3/2}}\approx 1.225}$,^[2] the structure would be topologically tetrahedrally close-packed.^[3] At this size ratio, the structure has an overall packing volume density of 0.710^[4] Compounds found in Laves phases typically have an atomic size ratio between 1.05 and 1.67.^[3] Analogues of Laves phases can be formed by the self-assembly of a colloidal dispersion of two sizes of sphere.^[2]

References

1. The Laves Phase Structures. nrl.navy.mil. Accessed on 2009-2-26.
2. Hynninen, A. P.; Thijssen, J. H. J.; Vermolen, E. C. M.; Dijkstra, M.; Van Blaaderen, A. (2007). "Self-assembly route for photonic crystals with a bandgap in the visible region". Nature Materials. 6 (3): 202–205. Bibcode:2007NatMa...6..202H. doi:10.1038/nmat1841. PMID 17293851.
3. Zhu, J. H.; Liu, C. T.; Pike, L. M.; Liaw, P. K. (1999). "A thermodynamic interpretation of the size-ratio limits for Laves phase formation". Metallurgical and Materials Transactions A. 30 (5): 1449. doi:10.1007/s11661-999-0292-5.
4. Murray, M. J.; Sanders, J. V. (1980). "Close-packed structures of spheres of two different sizes II. The packing densities of likely arrangements". Philosophical Magazine A. 42 (6): 721. doi:10.1080/01418618008239380.