List of centroids

The following is a list of centroids of various two-dimensional objects. A centroid of an object $X$ in $n$-dimensional space is the intersection of all hyperplanes that divide $X$ into two parts of equal moment about the hyperplane. Informally, it is the "average" of all points of $X$. For an object of uniform composition (mass, density, etc.) the centroid of a body is also its centre of mass. In the case of two-dimensional objects shown below, the hyperplanes are simply lines.

Centroids

Shape	Figure	${\bar {x}}$	${\bar {y}}$	Area
Right-triangular area		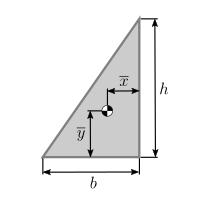${\frac {b}{3}}$	${\frac {h}{3}}$	${\frac {bh}{2}}$
Quarter-circular area[1]		${\displaystyle \frac{4r}{3\pi}}$	${\displaystyle \frac{4r}{3\pi}}$	${\frac {\pi r^{2}}{4}}$
Semicircular area[2]		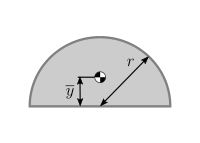$\,\!0$	${\displaystyle \frac{4r}{3\pi}}$	${\frac {\pi r^{2}}{2}}$
Quarter-elliptical area		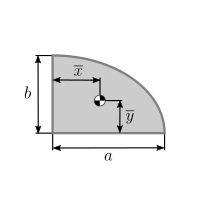${\frac {4a}{3\pi }}$	${\frac {4b}{3\pi }}$	${\frac {\pi ab}{4}}$
Semielliptical area		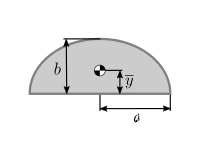$\,\!0$	${\frac {4b}{3\pi }}$	${\frac {\pi ab}{2}}$
Semiparabolic area The area between the curve $y={\frac {h}{b^{2}}}x^{2}$ and the $\,\!y$ axis, from $\,\!x=0$ to $\,\!x=b$		${\frac {3b}{8}}$	${\frac {3h}{5}}$	${\frac {2bh}{3}}$
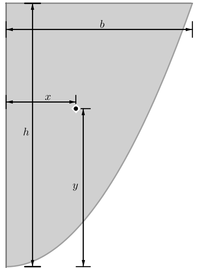Parabolic area	The area between the curve $\,\!y={\frac {h}{b^{2}}}x^{2}$ and the line $\,\!y=h$	$\,\!0$	${\frac {3h}{5}}$	${\frac {4bh}{3}}$
Parabolic spandrel	The area between the curve $\,\!y={\frac {h}{b^{2}}}x^{2}$ and the $\,\!x$ axis, from $\,\!x=0$ to $\,\!x=b$	${\frac {3b}{4}}$	${\frac {3h}{10}}$	${\frac {bh}{3}}$
General spandrel	The area between the curve $y={\frac {h}{b^{n}}}x^{n}$ and the $\,\!x$ axis, from $\,\!x=0$ to $\,\!x=b$	${\frac {n+1}{n+2}}b$	${\frac {n+1}{4n+2}}h$	${\frac {bh}{n+1}}$
Circular sector		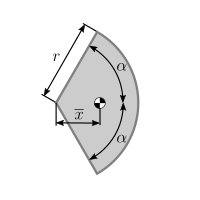${\displaystyle {\frac {2r\sin(\alpha )}{3\alpha }}}$	$\,\!0$	${\displaystyle \,\!\alpha r^{2}}$
Circular segment		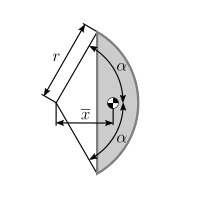${\displaystyle {\frac {4r\sin ^{3}(\alpha )}{3(2\alpha -\sin(2\alpha ))}}}$	$\,\!0$	${\displaystyle {\frac {r^{2}}{2}}(2\alpha -\sin(2\alpha ))}$
Quarter-circular arc	The points on the circle $\,\!x^{2}+y^{2}=r^{2}$ and in the first quadrant	${\frac {2r}{\pi }}$	${\frac {2r}{\pi }}$	$L={\frac {\pi r}{2}}$
Semicircular arc	The points on the circle $\,\!x^{2}+y^{2}=r^{2}$ and above the $\,\!x$ axis	$\,\!0$	${\frac {2r}{\pi }}$	$L=\,\!\pi r$
Arc of circle	The points on the curve (in polar coordinates) $\,\!r=\rho$, from $\,\!\theta =-\alpha$ to $\,\!\theta =\alpha$	${\frac {\rho \sin(\alpha )}{\alpha }}$	$\,\!0$	$L=\,\!2\alpha \rho$

See also

• List of moments of inertia
• List of second moments of area

References

1. "Quarter Circle". eFunda. Retrieved 23 April 2016.
2. "Circular Half". eFunda. Retrieved 23 April 2016.

External links

• http://www.engineering.com/Library/ArticlesPage/tabid/85/articleType/ArticleView/articleId/109/Centroids-of-Common-Shapes.aspx
• http://www.efunda.com/math/areas/IndexArea.cfm