Lorentz scalar

In physics, a Lorentz scalar is a scalar which is invariant under a Lorentz transformation. A Lorentz scalar may be generated from multiplication of vectors or tensors. While the components of vectors and tensors are in general altered by Lorentz transformations, scalars remain unchanged.

A Lorentz scalar is not necessarily a scalar in the strict sense of being a (0,0)-tensor, that is, invariant under any base transformation. For example, the determinant of the matrix of base vectors is a number that is invariant under Lorentz transformations, but it is not invariant under any base transformation.

Simple scalars in special relativity

The length of a position vector

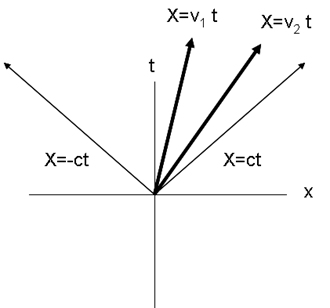
In special relativity the location of a particle in 4-dimensional spacetime is given by

$x^{{\mu }}=(ct,{\mathbf {x}})$

where ${\mathbf {x}}={\mathbf {v}}t$ is the position in 3-dimensional space of the particle, $\mathbf {v}$ is the velocity in 3-dimensional space and $c$ is the speed of light.

The "length" of the vector is a Lorentz scalar and is given by

$x_{{\mu }}x^{{\mu }}=\eta _{{\mu \nu }}x^{{\mu }}x^{{\nu }}=(ct)^{2}-{\mathbf {x}}\cdot {\mathbf {x}}\ {\stackrel {{\mathrm {def}}}{=}}\ (c\tau )^{2}$

where $\tau$ is the proper time as measured by a clock in the rest frame of the particle and the Minkowski metric is given by

$\eta ^{{\mu \nu }}=\eta _{{\mu \nu }}={\begin{pmatrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}}$.

This is a time-like metric.

Often the alternate signature of the Minkowski metric is used in which the signs of the ones are reversed.

$\eta ^{{\mu \nu }}=\eta _{{\mu \nu }}={\begin{pmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}$.

This is a space-like metric.

In the Minkowski metric the space-like interval $s$ is defined as

$x_{{\mu }}x^{{\mu }}=\eta _{{\mu \nu }}x^{{\mu }}x^{{\nu }}={\mathbf {x}}\cdot {\mathbf {x}}-(ct)^{2}\ {\stackrel {{\mathrm {def}}}{=}}\ s^{2}$.

We use the space-like Minkowski metric in the rest of this article.

The length of a velocity vector

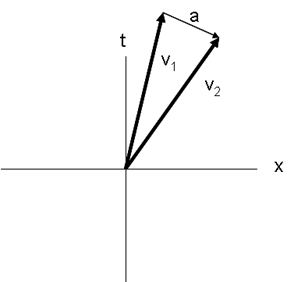
The velocity in spacetime is defined as

$v^{{\mu }}\ {\stackrel {{\mathrm {def}}}{=}}\ {dx^{{\mu }} \over d\tau }=\left(c{dt \over d\tau },{dt \over d\tau }{d{\mathbf {x}} \over dt}\right)=\left(\gamma c,\gamma {{\mathbf {v}}}\right)=\gamma \left(c,{{\mathbf {v}}}\right)$

where

$\gamma \ {\stackrel {{\mathrm {def}}}{=}}\ {1 \over {{\sqrt {1-{{{\mathbf {v}}\cdot {\mathbf {v}}} \over c^{2}}}}}}$.

The magnitude of the 4-velocity is a Lorentz scalar,

$v_{{\mu }}v^{{\mu }}=-c^{2}\,$.

Hence, c is a Lorentz scalar.

The inner product of acceleration and velocity

The 4-acceleration is given by

$a^{{\mu }}\ {\stackrel {{\mathrm {def}}}{=}}\ {dv^{{\mu }} \over d\tau }$.

The 4-acceleration is always perpendicular to the 4-velocity

$0={1 \over 2}{d \over d\tau }\left(v_{{\mu }}v^{{\mu }}\right)={dv_{{\mu }} \over d\tau }v^{{\mu }}=a_{{\mu }}v^{{\mu }}$.

Therefore, we can regard acceleration in spacetime as simply a rotation of the 4-velocity. The inner product of the acceleration and the velocity is a Lorentz scalar and is zero. This rotation is simply an expression of energy conservation:

${dE \over d\tau }={\mathbf {F}}\cdot {{\mathbf {v}}}$

where $E$ is the energy of a particle and $\mathbf {F}$ is the 3-force on the particle.

Energy, rest mass, 3-momentum, and 3-speed from 4-momentum

The 4-momentum of a particle is

$p^{{\mu }}=mv^{{\mu }}=\left(\gamma mc,\gamma {m{\mathbf {v}}}\right)=\left(\gamma mc,{{\mathbf {p}}}\right)=\left({E \over c},{{\mathbf {p}}}\right)$

where $m$ is the particle rest mass, $\mathbf {p}$ is the momentum in 3-space, and

$E=\gamma mc^{2}\,$

is the energy of the particle.

Measurement of the energy of a particle

Consider a second particle with 4-velocity $u$ and a 3-velocity ${\mathbf {u}}_{2}$. In the rest frame of the second particle the inner product of $u$ with $p$ is proportional to the energy of the first particle

$p_{{\mu }}u^{{\mu }}=-{E_{1}}$

where the subscript 1 indicates the first particle.

Since the relationship is true in the rest frame of the second particle, it is true in any reference frame. $E_{1}$, the energy of the first particle in the frame of the second particle, is a Lorentz scalar. Therefore,

${E_{1}}=\gamma _{1}\gamma _{2}m_{1}c^{2}-\gamma _{2}{\mathbf {p}}_{1}\cdot {\mathbf {u}}_{2}$

in any inertial reference frame, where $E_{1}$ is still the energy of the first particle in the frame of the second particle .

Measurement of the rest mass of the particle

In the rest frame of the particle the inner product of the momentum is

$p_{{\mu }}p^{{\mu }}=-(mc)^{2}\,$.

Therefore, the rest mass (m) is a Lorentz scalar. The relationship remains true independent of the frame in which the inner product is calculated. In many cases the rest mass is written as $m_{0}$ to avoid confusion with the relativistic mass, which is $\gamma m_{{0}}$

Measurement of the 3-momentum of the particle

Note that

$\left(p_{{\mu }}u^{{\mu }}/c\right)^{2}+p_{{\mu }}p^{{\mu }}={E_{1}^{2} \over c^{2}}-(mc)^{2}=\left(\gamma _{1}^{2}-1\right)(mc)^{2}=\gamma _{1}^{2}{{{\mathbf {v}}_{1}\cdot {\mathbf {v}}_{1}}}m^{2}={\mathbf {p}}_{1}\cdot {\mathbf {p}}_{1}$.

The square of the magnitude of the 3-momentum of the particle as measured in the frame of the second particle is a Lorentz scalar.

Measurement of the 3-speed of the particle

The 3-speed, in the frame of the second particle, can be constructed from two Lorentz scalars

$v_{1}^{2}={\mathbf {v}}_{1}\cdot {\mathbf {v}}_{1}={{{\mathbf {p}}_{1}\cdot {\mathbf {p}}_{1}c^{4}} \over {E_{1}^{2}}}$.

More complicated scalars

Scalars may also be constructed from the tensors and vectors, from the contraction of tensors, or combinations of contractions of tensors and vectors.

References

• Misner, Charles; Thorne, Kip S. & Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. ISBN 0-7167-0344-0.
• Landau, L. D. & Lifshitz, E. M. (1975). Classical Theory of Fields (Fourth Revised English Edition). Oxford: Pergamon. ISBN 0-08-018176-7.