Majority logic decoding
In error detection and correction, majority logic decoding is a method to decode repetition codes, based on the assumption that the largest number of occurrences of a symbol was the transmitted symbol.
Theory
In a binary alphabet made of 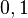 , if a
, if a 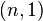 repetition code is used, then each input bit is mapped to the code word as a string of
repetition code is used, then each input bit is mapped to the code word as a string of 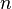 -replicated input bits. Generally
-replicated input bits. Generally 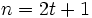 , an odd number.
, an odd number.
The repetition codes can detect up to ![[n/2]](../I/m/1df61e7f2446684a7a300e9420d62011.png) transmission errors. Decoding errors occur when the more than these transmission errors occur. Thus, assuming bit-transmission errors are independent, the probability of error for a repetition code is given by
transmission errors. Decoding errors occur when the more than these transmission errors occur. Thus, assuming bit-transmission errors are independent, the probability of error for a repetition code is given by 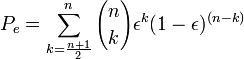 , where
, where  is the error over the transmission channel.
is the error over the transmission channel.
Algorithm
Assumptions
The code word is 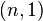 , where
, where 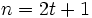 , an odd number.
, an odd number.
- Calculate the
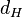 Hamming weight of the repetition code.
Hamming weight of the repetition code. - if
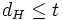 , decode code word to be all 0's
, decode code word to be all 0's - if
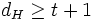 , decode code word to be all 1's
, decode code word to be all 1's
Example
In a 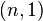 code, if R=[1 0 1 1 0], then
it would be decoded as,
code, if R=[1 0 1 1 0], then
it would be decoded as,
-
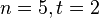 ,
, 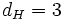 , so R'=[1 1 1 1 1]
, so R'=[1 1 1 1 1] - Hence the transmitted message bit was 1.
References
- Rice University, http://cnx.rice.edu/content/m0071/latest/