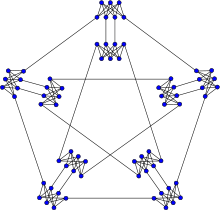
Meredith graph

Meredith graph
The Meredith graph
Named after	G. H. Meredith
Vertices	70
Edges	140
Radius	7
Diameter	8
Girth	4
Automorphisms	38698352640
Chromatic number	3
Chromatic index	5
Properties	Eulerian

In the mathematical field of graph theory, the Meredith graph is a 4-regular undirected graph with 70 vertices and 140 edges discovered by Guy H. J. Meredith in 1973.^[1]

The Meredith graph is 4-vertex-connected and 4-edge-connected, has chromatic number 3, chromatic index 5, radius 7, diameter 8, girth 4 and is non-hamiltonian.^[2]

Published in 1973, it provides a counterexample to the Crispin Nash-Williams conjecture that every 4-regular 4-vertex-connected graph is Hamiltonian.^[3][4] However, W. T. Tutte showed that all 4-connected planar graphs are hamiltonian.^[5]

The characteristic polynomial of the Meredith graph is $(x-4)(x-1)^{{10}}x^{{21}}(x+1)^{{11}}(x+3)(x^{2}-13)(x^{6}-26x^{4}+3x^{3}+169x^{2}-39x-45)^{4}$.

Gallery

• 
  The chromatic number of the Meredith graph is 3.
• 
  The chromatic index of the Meredith graph is 5.

References

1. Weisstein, Eric W. "Meredith graph". MathWorld.
2. Bondy, J. A. and Murty, U. S. R. "Graph Theory". Springer, p. 470, 2007.
3. Meredith, G. H. J. "Regular 4-Valent 4-Connected Nonhamiltonian Non-4-Edge-Colorable Graphs." J. Combin. Th. B 14, 55-60, 1973.
4. Bondy, J. A. and Murty, U. S. R. "Graph Theory with Applications". New York: North Holland, p. 239, 1976.
5. Tutte, W.T., ed., Recent Progress in Combinatorics. Academic Press, New York, 1969.