Meyer wavelet

The Meyer wavelet is an orthogonal wavelet proposed by Yves Meyer. It is infinitely differentiable with infinite support and defined in frequency domain in terms of function $\nu$ as:

$\Psi ( \omega) := \begin{cases} \frac {1}{\sqrt{2\pi}} \sin\left(\frac {\pi}{2} \nu \left(\frac{3|\omega|}{2\pi} -1\right)\right) e^{j\omega/2} & \text{if } 2 \pi /3<|\omega|< 4 \pi /3, \\ \frac {1}{\sqrt{2\pi}} \cos\left(\frac {\pi}{2} \nu \left(\frac{3| \omega|}{4 \pi}-1\right)\right) e^{j \omega/2} & \text{if } 4 \pi /3<| \omega|< 8 \pi /3, \\ 0 & \text{otherwise}, \end{cases}$

where:

$\nu (x) := \begin{cases} 0 & \text{if } x < 0, \\ x & \text{if } 0< x < 1, \\ 1 & \text{if } x > 1. \end{cases}$

There are many different ways for defining this auxiliary function, which yields variants of the Meyer wavelet. For instance, another standard implementation adopts

$\nu (x) := \begin{cases} {x^4}(35-84x+70{x^2}-20{x^3}) & \text{if } 0< x < 1, \\ 0 & \text{otherwise}. \end{cases}$

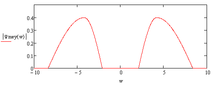
Spectrum of the Meyer wavelet.

The Meyer scale function is given by:

$\Phi ( \omega) := \begin{cases} \frac {1}{\sqrt{2\pi}} & \text{if } | \omega|< 2 \pi /3, \\ \frac {1}{\sqrt{2\pi}} \cos\left(\frac {\pi}{2} \nu \left(\frac{3|\omega|} {2\pi}-1\right) \right) & \text{if } 2\pi/3<|\omega|< 4\pi/3, \\ 0 & \text{otherwise}. \end{cases}$

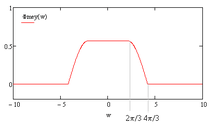
Meyer scale function.

In the time-domain, the waveform of the Meyer mother-wavelet has the shape as shown in the following figure:

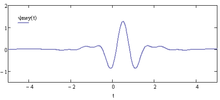
Meyer wavelet.

In 2015, Victor Vermehren Valenzuela and H. M. de Oliveira gave the explicitly expressions of Meyer wavelet and scale functions:

${\displaystyle \phi (t)=\left\{{\begin{array}{ll}{\frac {2}{3}}+{\frac {4}{3\pi }}&t=0,\\{\frac {\sin({\frac {2\pi }{3}}t)+{\frac {4}{3}}t\cos({\frac {4\pi }{3}}t)}{\pi t-{\frac {16\pi }{9}}t^{3}}}&otherwise,\end{array}}\right.}$

and

${\displaystyle \psi (t)=\psi _{1}(t)+\psi _{2}(t)}$

where

${\displaystyle \psi _{1}(t)={\frac {{\frac {4}{3\pi }}(t-{\frac {1}{2}})\cos[{\frac {2\pi }{3}}(t-{\frac {1}{2}})]-{\frac {1}{\pi }}\sin[{\frac {4\pi }{3}}(t-{\frac {1}{2}})]}{(t-{\frac {1}{2}})-{\frac {16}{9}}(t-{\frac {1}{2}})^{3}}},}$

and

${\displaystyle \psi _{2}(t)={\frac {{\frac {8}{3\pi }}(t-{\frac {1}{2}})\cos[{\frac {8\pi }{3}}(t-{\frac {1}{2}})]+{\frac {1}{\pi }}\sin[{\frac {4\pi }{3}}(t-{\frac {1}{2}})]}{(t-{\frac {1}{2}})-{\frac {64}{9}}(t-{\frac {1}{2}})^{3}}}.}$

References

• Meyer (Y.), Ondelettes et Opérateurs, Hermann, 1990.
• Daubechies, (I.), Ten lectures on wavelets, CBMS-NSF conference series in applied mathematics, SIAM Ed., pp. 117–119, 137, 152, 1992.
• Victor Vermehren Valenzuela and H. M. de Oliveira, Close expressions for Meyer Wavelet and Scale Function, 2015, p.4.

External links

• wavelet toolbox
• Matlab implementation