Mojette Transform

The Mojette Transform is an application of discrete geometry. More specifically, it is a discrete and exact version of the Radon transform, thus a projection operator.

The IRCCyN laboratory - UMR CNRS 6597 in Nantes, France has been developing it since 1994.

The first characteristic of the Mojette Transform is using only additions and subtractions. The second characteristic is that the Mojette Transform is redundant, spreading the initial geometrical information into several projections.

This transform uses discrete geometry in order to dispatch information onto a discrete geometrical support. This support is then projected by the Mojette operator along discrete directions. When enough projections are available, the initial information can be reconstructed.

The Mojette transform has been already used in numerous applications domains:

History

After one year of research, the first communication introducing the Mojette Transform was held in May 1995 in the first edition of CORESA National Congress CCITT Rennes. Many others will follow it for 18 years of existence. In 2011, the book The Mojette Transform: Theory and Applications at ISTE-Wiley was well received by the scientific community. All this support has encouraged the IRCCyN research team to continue the research on this topic.

Jeanpierre Guédon, professor and inventor of the transform called it: "Mojette Transform". The word "Mojette" comes from the name of white beans in Vendee, originally written "Moghette" or "Mojhette". In many countries, bean is a basic educational tool representing an exact unit that teaches visually additions and subtractions. Therefore, the choice of the name "Mojette" serves to emphasize the fact that the transform uses only exact unit in additions and subtractions.

There is an old French saying in Vendee: "counting his mojettes", meaning to know how to count his money. It is quite amazing that in the English-speaking world, the words "bean counter" refers to a non-zealous official making additions. An old English expression says "he knows how many beans make five", which means: "He knows his stuff".

The original purpose of the Mojette Transform was to create a discrete tool to divide the Fourier plane into angular and radial sectors. The first attempt of application was the psychovisual encoding of image, reproducing the human vision channel. However, it was never realized.

Mathematics

The "raw" transform Mojette definition is this:

The following figure 1 helps to explain the “raw” transform Mojette.

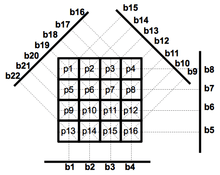
Figure 1 : 4x4 grid with 16 pixels, 4 projections and 22 bins

We start with the function f represented by 16 pixels from p1 to p16. The possible values of the function at the point (k, l) are different according to the applications. This can be a binary value of 0 or 1 that it often used to differentiate the object and the background. This can be a ternary value as in the Mojette game. This can be also a finite set of integers value from 0 to (n-1), or more often we take a set of cardinality equal to a power of 2 or a prime number. But it can be integers and real numbers with an infinite number of possibilities, even though this idea has never been used.

With the index "k" as "kolumn" and “l” as a “line”, we define a Cartesian coordinate system. But here we will only need the integer coordinates. On Figure 2, we have arbitrarily chosen the left bottom point as the origin (0,0) and the direction of the two axes. The coordinates of each pixel are denoted in red on Figure 2.

Figure 2 : Mark of 4x4 grid and projections

For the projections, the coordinate system is derived from the one of the grid. Indeed it meets two requirements: 1) The pixel (0,0) is always projected on the point 0 of the projection (this is a consequence of linearity of the Mojette operator) 2) The direction of the projection is fixed "counterclockwise" as in trigonometry when going from 0 ° to 180 °.

Altogether, it necessarily gives the positions of the bins like the ones in blue color on the Figure 2. Let’s head back to the formula (1): the red dots correspond to the index (k, l) and the blue dots to the index b. The only elements remaining to clarify are the (p, q) values.

These two values (p, q) are precisely those characterizing the Mojette Transform. They define the projection angle. Figure 3 shows colored arrows corresponding with the color code to the projection indexed by (p, q). For the 90° angle, the projection is shown below the grid for convenience but the direction is upward. Table 1 shows the correspondence between the angles in degrees and the values of p and q.

Figure 3: Projections of direction (p, q) of the 4x4 grid
0° p=1 q=0 b-l=0
45° p=1 q=1 b+k-l=0
90° p=0 q=1 b+k=0
135° p=-1 q=1 b+k+l=0

Table 1 : The correspondence of the angles projections with direction equation b + qk - pl = 0

The only valid Mojette angles are given by the following rules: 1) An angle is given by the direction of projection in line and column 2) A direction is composed of two integers (p, q) with gcd (p, q) = 1 3) An angle is always between 0 and 180 °, which means that q is never negative

These rules ensure the uniqueness in the correspondence of an angle and (p, q) values. For example, the 45 ° angle, the Rule 2 forbid to define the angle pairs (2,2) or (3,3) and Rule 3 prohibits to use (-2, -2) and (-1, -1). Only the angle (p = 1, q = 1) satisfies the three rules.

Applications & Achievements

The distributed storage disk or network

The most important area of application using the "Mojette Transform" is distributed storage. Particularly, this method is used in RozoFS, an open-source distributed file system. In this application, the "Mojette Transform" is used as an erasure code in order to provide reliability, while significantly reducing the total amount of stored data when compared to classical techniques like replication (typically by a factor of 2). Thus, it significantly reduces the cost of the storage cluster in terms of hardware, maintenance or energy consumption for example.

In 2010, Pierre Evenou, research engineer of the IVC team IRCCyN laboratory, decided to create the start-up Fizians (currently known as Rozo Systems) using this application. The start-up offers storage solutions in cloud computing, virtualization, storage servers, file servers, backup and archiving.

Networks packets transfer

Thanks to the redundancy of the transform, sent packets can be fragmented without loss. Additionally, the fact of using only additions and subtractions increases the speed of information transmission. Finally, the information cannot be reconstructed without having the initial angle of the projections, so it also provides data security.

This application has been selected by Thales Cholet for its ad hoc network (using wireless network and terminals to transmit messages between them) in order to secure the information and has multiple paths between the source and destination. In 2002, the start-up PIBI has used this technology to provide secure Internet payment services.

The Medical tomography

In the field of medical imaging, the properties of the “Transform Mojette” create a direct mapping and solve the missing wedge problem. However, the image acquisition using the Mojette transform has not been yet developed. The problem of obtaining exact “Mojette” values while using approximated data acquisition has been studied but has to be continued. Besides, the post-processing of medical images is doing well since data acquisition is already done.

These results are used by the company Keosys in 2001 with Jerome Fortineau and the company Qualiformed created in 2006 by Stephen Beaumont. Prof. Guédon and the IRCCyN laboratory were heavily involved in the creation of these two companies. The companies have already financed several PhD students and participated in research projects in order to continue the development of the application in medical tomography. The results have led to apply patents and implementation on their equipment of image processing.

The watermarking and image encryption

Cryptography and watermarking were also part of the research conducted in the IRCCyN laboratory. It provides solutions for security and authentication.

In cryptography, the instability of the transformed Mojette secures data. The fact that the transform is exact encrypts information and allows no deviation even minimal. For watermarking, the transform is very effective in fingerprinting. By inserting "Mojette Transform" marks in images, one can authenticate documents using the same properties as in cryptography.

References

This article is issued from Wikipedia - version of the 2/12/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.