Octant (solid geometry)

Three axial planes (x=0, y=0, z=0) divide space into eight equal octant domains, each with a coordinate signs from (-,-,-) to (+,+,+).
An octant in solid geometry is one of the eight divisions of a Euclidean three-dimensional coordinate system defined by the signs of the coordinates. It is similar to the two-dimensional quadrant and the one-dimensional ray.[1]
The generalization of an octant is called orthant.
Naming and Numbering
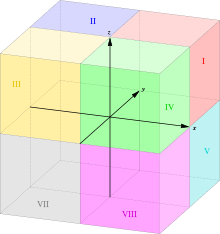
For z > 0, the octants have the same numbers as the corresponding quadrants in the plane.
A convention for naming an octant is to give its list of signs, e.g. ( + - - ) or ( - + - ). Octant ( + + + ) is sometimes referred to as the first octant, although similar ordinal name descriptors are not defined for the other seven octants. The advantages of using the ( + - - ) notation are its unambiguousness, and extensibility for higher dimensions.
| Number | Name | x | y | z | Octal (+=0,zyx) | Octal (+=1,zyx) |
|---|---|---|---|---|---|---|
| I | top-front-right | + | + | + | 0 | 7 |
| II | top-back-right | − | + | + | 1 | 6 |
| III | top-back-left | − | − | + | 3 | 4 |
| IV | top-front-left | + | − | + | 2 | 5 |
| V | bottom-front-right | + | + | − | 4 | 3 |
| VI | bottom-back-right | − | + | − | 5 | 2 |
| VII | bottom-back-left | − | − | − | 7 | 0 |
| VIII | bottom-front-left | + | − | − | 6 | 1 |
References
See also
This article is issued from Wikipedia - version of the 11/9/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.