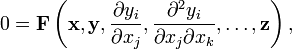Partial differential algebraic equation

In mathematics a partial differential algebraic equation (PDAE) set is an incomplete system of partial differential equations that is closed with a set of algebraic equations.

Definition

A general PDAE is defined as:

$0 = \mathbf F \left( \mathbf x, \mathbf y, \frac{\partial y_i}{\partial x_j}, \frac{\partial^2 y_i}{\partial x_j \partial x_k}, \ldots, \mathbf z \right),$

where:

• F is a set of arbitrary functions;
• x is a set of independent variables;
• y is a set of dependent variables for which partial derivatives are defined; and
• z is a set of dependent variables for which no partial derivatives are defined.

The relationship between a PDAE and a partial differential equation (PDE) is analogous to the relationship between an ordinary differential equation (ODE) and a differential algebraic equation (DAE).

PDAEs of this general form are challenging to solve. Simplified forms are studied in more detail in the literature.^[1][2][3] Even as recently as 2000, the term "PDAE" has been handled as unfamiliar by those in related fields.^[4]

Solution methods

Semi-discretization is a common method for solving PDAEs whose independent variables are those of time and space, and has been used for decades.^[5][6] This method involves removing the spatial variables using a discretization method, such as the finite volume method, and incorporating the resulting linear equations as part of the algebraic relations. This reduces the system to a DAE, for which conventional solution methods can be employed.

References

1. Wagner, Y. 2000. "A further index concept for linear PDAEs of hyperbolic type," Mathematics and Computers in Simulation, v. 53, pp. 287–291.
2. W. S. Martinson, P. I. Barton. (2002) "Index and characteristic analysis of linear PDAE systems," Siam Journal on Scientific Computing, v. 24, n. 3, pp. 905–923.
3. Lucht, W.; Strehmel, K.. 1998. "Discretization based indices for semilinear partial differential algebraic equations," Applied Numerical Mathematics, v. 28, pp. 371–386.
4. Simeon, B.; Arnold, M.. 2000. "Coupling DAEs and PDEs for simulating the interaction of pantograph and catenary," Mathematical and Computer Modelling of Dynamical Systems, v. 6, pp. 129–144.
5. Jacob, J.; Le Lann, J; Pinguad, H.; Capdeville, B.. 1996. "A generalized approach for dynamic modelling and simulation of biofilters: application to waste-water denitrification," Chemical Engineering Journal, v. 65, pp. 133–143.
6. de Dieuvleveult, C.; Erhel, J.; Kern, M.. 2009. "A global strategy for solving reactive transport equations," Journal of Computational Physics, v. 228, pp. 6395–6410.