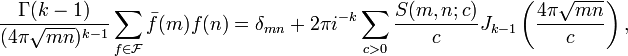Petersson trace formula
In analytic number theory, the Petersson trace formula is a kind of orthogonality relation between coefficients of a holomorphic modular form. It is a specialization of the more general Kuznetsov trace formula.
In its simplest form the Petersson trace formula is as follows. Let 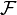 be an orthonormal basis of
be an orthonormal basis of 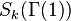 , the space of cusp forms of weight
, the space of cusp forms of weight 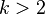 on
on 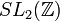 . Then for any positive integers
. Then for any positive integers 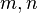 we have
we have
where 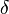 is the Kronecker delta function,
is the Kronecker delta function, 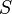 is the Kloosterman sum and
is the Kloosterman sum and  is the Bessel function of the first kind.
is the Bessel function of the first kind.
References
- Henryk Iwaniec: Topics in Classical Automorphic Forms. Graduate Studies in Mathematics 17, American Mathematics Society, Providence, RI, 1991.
This article is issued from Wikipedia - version of the 8/8/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.