Plethystic substitution
Plethystic substitution is a shorthand notation for a common kind of substitution in the algebra of symmetric functions and that of symmetric polynomials. It is essentially basic substitution of variables, but allows for a change in the number of variables used.
Definition
The formal definition of plethystic substitution relies on the fact that the ring of symmetric functions 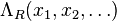 is generated as an R-algebra by the power sum symmetric functions
is generated as an R-algebra by the power sum symmetric functions
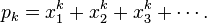
For any symmetric function 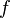 and any formal sum of monomials
and any formal sum of monomials 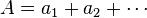 , the plethystic substitution f[A] is the formal series obtained by making the substitutions
, the plethystic substitution f[A] is the formal series obtained by making the substitutions
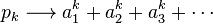
in the decomposition of 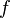 as a polynomial in the pk's.
as a polynomial in the pk's.
Examples
If 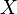 denotes the formal sum
denotes the formal sum  , then
, then ![f[X]=f(x_1,x_2,\ldots)](../I/m/e249fe46001d9de8f891257fc576ecf1.png) .
.
One can write 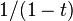 to denote the formal sum
to denote the formal sum 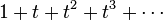 , and so the plethystic substitution
, and so the plethystic substitution ![f[1/(1-t)]](../I/m/e3f1528e541a66887ebfdcd8697aaf1a.png) is simply the result of setting
is simply the result of setting 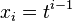 for each i. That is,
for each i. That is,
![f\left[\frac{1}{1-t}\right]=f(1,t,t^2,t^3,\ldots)](../I/m/2d6224efbbf4cbe960df7371be40d715.png) .
.
Plethystic substitution can also be used to change the number of variables: if 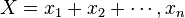 , then
, then ![f[X]=f(x_1,\ldots,x_n)](../I/m/770ca7e79ffd50580f59782c1fef7f27.png) is the corresponding symmetric function in the ring
is the corresponding symmetric function in the ring 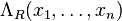 of symmetric functions in n variables.
of symmetric functions in n variables.
Several other common substitutions are listed below. In all of the following examples,  and
and 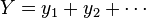 are formal sums.
are formal sums.
- If
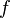 is a homogeneous symmetric function of degree
is a homogeneous symmetric function of degree 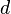 , then
, then
![f[tX]=t^d f(x_1,x_2,\ldots)](../I/m/3bcb01cbb5b42ee3cfa8ccbd98c7f0c2.png)
- If
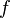 is a homogeneous symmetric function of degree
is a homogeneous symmetric function of degree 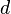 , then
, then
![f[-X]=(-1)^d \omega f(x_1,x_2,\ldots)](../I/m/88f78e55e7b26abf858b8cbcb668904e.png) ,
where
,
where 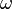 is the well-known involution on symmetric functions that sends a Schur function
is the well-known involution on symmetric functions that sends a Schur function 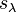 to the conjugate Schur function
to the conjugate Schur function 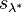 .
.
- The substitution
![S:f\mapsto f[-X]](../I/m/2e2f2db7a58f9ddcd1131e47893dc924.png) is the antipode for the Hopf algebra structure on the Ring of symmetric functions.
is the antipode for the Hopf algebra structure on the Ring of symmetric functions. ![p_n[X+Y]=p_n[X]+p_n[Y]](../I/m/96229814f579bf2d7de11463adb30641.png)
- The map
![\Delta: f\mapsto f[X+Y]](../I/m/ce1c6e9e4c1eaee6fb01a3ea60fb63d7.png) is the coproduct for the Hopf algebra structure on the ring of symmetric functions.
is the coproduct for the Hopf algebra structure on the ring of symmetric functions. ![h_n\left[X(1-t)\right]](../I/m/49d057f8f9b697e4175044faf1989b0f.png) is the alternating Frobenius series for the exterior algebra of the defining representation of the symmetric group, where
is the alternating Frobenius series for the exterior algebra of the defining representation of the symmetric group, where 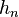 denotes the complete homogeneous symmetric function of degree
denotes the complete homogeneous symmetric function of degree 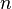 .
.![h_n\left[X/(1-t)\right]](../I/m/bb79ad8def606359c92bf217d4487ca9.png) is the Frobenius series for the symmetric algebra of the defining representation of the symmetric group.
is the Frobenius series for the symmetric algebra of the defining representation of the symmetric group.
External links
- Combinatorics, Symmetric Functions, and Hilbert Schemes (Haiman, 2002)
References
- M. Haiman, Combinatorics, Symmetric Functions, and Hilbert Schemes, Current Developments in Mathematics 2002, no. 1 (2002), pp. 39–111.