Positive invariant set
In mathematical analysis, a positively invariant set is a set with the following properties:
Given a dynamical system 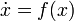 and trajectory
and trajectory 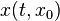 where
where 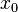 is the initial point. Let
is the initial point. Let 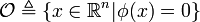 where
where 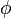 is a real valued function. The set
is a real valued function. The set 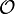 is said to be positively invariant if
is said to be positively invariant if 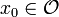 implies that
implies that 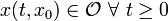
Intuitively, this means that once a trajectory of the system enters 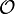 , it will never leave it again.
, it will never leave it again.
References
This article is issued from Wikipedia - version of the 9/10/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.