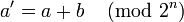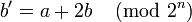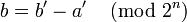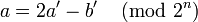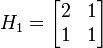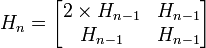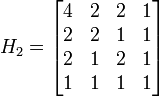Pseudo-Hadamard transform

The pseudo-Hadamard transform is a reversible transformation of a bit string that provides cryptographic diffusion. See Hadamard transform.

The bit string must be of even length, so it can be split into two bit strings a and b of equal lengths, each of n bits. To compute the transform, a' and b', from these we use the equations:

$a' = a + b \, \pmod{2^n}\,$

$b' = a + 2b\, \pmod{2^n}\,$

To reverse this, clearly:

$b = b' - a' \, \pmod{2^n}$

$a = 2a' - b' \, \pmod{2^n}$

Generalization

The above equations can be expressed in matrix algebra, by considering a and b as two elements of a vector, and the transform itself as multiplication by a matrix of the form:

$H_1 = \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix}$

The inverse can then be derived by inverting the matrix.

However, the matrix can be generalised to higher dimensions, allowing vectors of any power-of-two size to be transformed, using the following recursive rule:

$H_n = \begin{bmatrix} 2 \times H_{n-1} & H_{n-1} \\ H_{n-1} & H_{n-1} \end{bmatrix}$

For example:

$H_2 = \begin{bmatrix} 4 & 2 & 2 & 1 \\ 2 & 2 & 1 & 1 \\ 2 & 1 & 2 & 1 \\ 1 & 1 & 1 & 1 \end{bmatrix}$

See also

• SAFER
• Twofish

References

• James Massey, "On the Optimality of SAFER+ Diffusion", 2nd AES Conference, 1999.
• Bruce Schneier, John Kelsey, Doug Whiting, David Wagner, Chris Hall, "Twofish: A 128-Bit Block Cipher", 1998.
• Helger Lipmaa. On Differential Properties of Pseudo-Hadamard Transform and Related Mappings. INDOCRYPT 2002, LNCS 2551, pp 48-61, 2002.

External links

• Fast Pseudo-Hadamard Transforms