Ramachandran plot

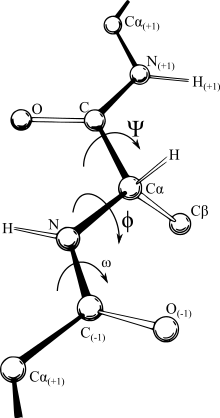
A Ramachandran plot (also known as a Ramachandran diagram or a [φ,ψ] plot), originally developed in 1963 by G. N. Ramachandran, C. Ramakrishnan, and V. Sasisekharan,[1] is a way to visualize energetically allowed regions for backbone dihedral angles ψ against φ of amino acid residues in protein structure. The figure at left illustrates the definition of the φ and ψ backbone dihedral angles[2] (called φ and φ' by Ramachandran). The ω angle at the peptide bond is normally 180°, since the partial-double-bond character keeps the peptide planar.[3] The figure at top right shows the allowed φ,ψ backbone conformational regions from the Ramachandran et al. 1963 and 1968 hard-sphere calculations: full radius in solid outline, reduced radius in dashed, and relaxed tau (N-Cα-C) angle in dotted lines.[4] Because dihedral angle values are circular and 0° is the same as 360°, the edges of the Ramachandran plot "wrap" right-to-left and bottom-to-top. For instance, the small strip of allowed values along the lower-left edge of the plot are a continuation of the large, extended-chain region at upper left.
Uses
A Ramachandran plot can be used in two somewhat different ways. One is to show in theory which values, or conformations, of the ψ and φ angles are possible for an amino-acid residue in a protein (as at top right). A second is to show the empirical distribution of datapoints observed in a single structure (as at right, here) in usage for structure validation, or else in a database of many structures (as in the lower 3 plots at left). Either case is usually shown against outlines for the theoretically favored regions.
Amino-acid preferences
One might expect that larger side chains would result in more restrictions and consequently a smaller allowable region in the Ramachandran plot. In practice, the major effect seen is that of the presence or absence of the methylene group at Cβ. Glycine has only a hydrogen atom for its side chain, with a much smaller van der Waals radius than the CH3, CH2, or CH group that starts the side chain of all other amino acids. Hence it is least restricted, and this is apparent in the Ramachandran plot for glycine (see Gly plot in gallery) for which the allowable area is considerably larger. In contrast, the Ramachandran plot for proline, with its 5-membered-ring side chain connecting Cα to backbone N, shows a limited number of possible combinations of ψ and φ (see Pro plot in gallery).
More recent updates
The first Ramachandran plot was calculated just after the first protein structure at atomic resolution was determined (myoglobin, in 1960[5]), although the conclusions were based on small-molecule crystallography of short peptides. Now, many decades later, there are tens of thousands of high-resolution protein structures determined by X-ray crystallography and deposited in the Protein Data Bank (PDB). Many studies have taken advantage of this data to produce more detailed and accurate φ,ψ plots (e.g., Morris et al. 1992;[6] Kleywegt & Jones 1996;[7] Hooft et al. 1997;[8] Hovmöller et al. 2002;[9] Lovell et al. 2003;[10] Anderson et al. 2005.[11] Ting et al. 2010[12]).
The three figures below show the datapoints from a large set of high-resolution structures and contours for favored and for allowed conformational regions for the general case (all amino acids except Gly, Pro, and pre-Pro), for Gly, and for Pro.[10] The most common regions are labeled: α for α helix, Lα for lefthanded helix, β for β-sheet, and ppII for polyproline II.
The Molecular Biophysics Unit at Indian Institute of Science celebrated 50 years of Ramachandran Map[13] by organizing International Conference on Biomolecular Forms and Functions from 8–11 January 2013.[14]
Related conventions
One can also plot the dihedral angles in polysaccharides (e.g. with CARP;[15]) and other polymers in this fashion. For the first two protein side-chain dihedral angles a similar plot is the Janin Plot.
Gallery
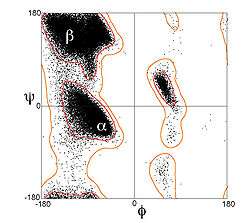 Ramachandran plot for the general case; data from Lovell 2003
Ramachandran plot for the general case; data from Lovell 2003 Ramachandran plot for Glycine
Ramachandran plot for Glycine Ramachandran plot for Proline
Ramachandran plot for Proline Ramachandran plot for pre-Proline
Ramachandran plot for pre-Proline
Software
- Web-based Structural Analysis tool for any uploaded PDB file, producing Ramachandran plots, computing dihedral angles and extracting sequence from PDB
- Web-based tool showing Ramachandran plot of any PDB entry
- MolProbity web service that produces Ramachandran plots and other validation of any PDB-format file
- SAVES (Structure Analysis and Verification) — uses WHATCHECK, PROCHECK, and does its own internal Ramachandran Plot
- STING
- Pymol with the DynoPlot extension
- VMD, distributed with dynamic Ramachandran plot plugin
- WHAT CHECK, the stand-alone validation routines from the WHAT IF software
- UCSF Chimera, found under the Model Panel.
- Sirius
- Swiss PDB Viewer
- TALOS
- Zeus molecular viewer — found under "Tools" menu, high quality plots with regional contours
- Procheck
- Neighbor-Dependent and Neighbor-Independent Ramachandran Probability Distributions[12]
See also PDB for a list of similar software.
References
- ↑ Ramachandran, G.N.; Ramakrishnan, C.; Sasisekharan, V. (1963). "Stereochemistry of polypeptide chain configurations". Journal of Molecular Biology. 7: 95–9. doi:10.1016/S0022-2836(63)80023-6. PMID 13990617.
- ↑ Richardson, J.S. (1981). "Anatomy and Taxonomy of Protein Structures". Advances in Protein Chemistry. Advances in Protein Chemistry. 34: 167–339. doi:10.1016/S0065-3233(08)60520-3. ISBN 9780120342341. PMID 7020376.
- ↑ Pauling, L.; Corey, H.R.; Branson, H. R. (1951). "The Structure of Proteins: Two Hydrogen-Bonded Helical Configurations of the Polypeptide Chain". Proceedings of the National Academy of Sciences of the United States of America. 37 (4): 205–211. doi:10.1073/pnas.37.4.205. PMC 1063337
 . PMID 14816373.
. PMID 14816373. - ↑ Ramachandran, G.N.; Sasiskharan, V. (1968). "Conformation of polypeptides and proteins". Advances in Protein Chemistry. Advances in Protein Chemistry. 23: 283–437. doi:10.1016/S0065-3233(08)60402-7. ISBN 9780120342235. PMID 4882249.
- ↑ Kendrew, J.C.; Dickerson, R.E.; Strandberg, B.E.; Hart, R.G.; Davies, D.R.; Phillips, D.C.; Shore, V.C. (1960). "Structure of myoglobin: a three-dimensional Fourier synthesis at 2Å resolution". Nature. 185 (4711): 422–427. doi:10.1038/185422a0. PMID 18990802.
- ↑ Morris, A.L.; MacArthur, M.W.; Hutchinson, E G.; Thornton, J.M. (1992). "Stereochemical quality of protein structure coordinates". Proteins: Structure, Function, and Genetics. 12 (4): 345–64. doi:10.1002/prot.340120407. PMID 1579569.
- ↑ Kleywegt, G.J.; Jones, T.A. (1996). "Phi/psi-chology: Ramachandran revisited". Structure. 4 (12): 1395–400. doi:10.1016/S0969-2126(96)00147-5. PMID 8994966.
- ↑ Hooft, R.W.W.; Sander, C.; Vriend, G. (1997). "Objectively judging the quality of a protein structure from a Ramachandran plot". Comput Appl Biosci. 13 (4): 425–430. doi:10.1093/bioinformatics/13.4.425. PMID 9283757.
- ↑ Hovmöller, S.; Zhou, T.; Ohlson, T. (2002). "Conformations of amino acids in proteins". Acta Crystallographica D. 58 (Pt 5): 768–76. doi:10.1107/S0907444902003359. PMID 11976487.
- 1 2 Lovell, S.C.; Davis, I.W.; Arendall, W.B.; De Bakker, P.I.W.; Word, J.M.; Prisant, M.G.; Richardson, J.S.; Richardson, D.C. (2003). "Structure validation by Cα geometry: ϕ,ψ and Cβ deviation". Proteins: Structure, Function, and Genetics. 50 (3): 437–50. doi:10.1002/prot.10286. PMID 12557186.
- ↑ Anderson RJ, Weng Z, Campbell RK, Jiang X (2005). "Main-chain conformational tendencies of amino acids". Proteins. 60 (4): 679–89. doi:10.1002/prot.20530. PMID 16021632.
- 1 2 Ting, D.; Wang, G.; Mitra, R.; Jordan, M.I.; Dunbrack, R.L. (2010). "Neighbor-dependent Ramachandran probability distributions of amino acids developed from a hierarchical Dirichlet process model". PLOS Computational Biology. 6 (4): e1000763. doi:10.1371/journal.pcbi.1000763. PMC 2861699
 . PMID 20442867.
. PMID 20442867. - ↑ "50th Anniversary of Ramachandran Plots". Professor Laurence A. Moran. Retrieved 17 January 2013.
- ↑ "ICBFF-2013". MBU, IISc, Bangalore. Retrieved 28 January 2013.
- ↑ Lütteke, T.; Frank, M.; von der Lieth, C.W. (2005). "Carbohydrate Structure Suite (CSS): analysis of carbohydrate 3D structures derived from the PDB". Nucleic Acids Res. 33 (Database issue): D242–246. doi:10.1093/nar/gki013. PMC 539967
 . PMID 15608187.
. PMID 15608187.
Further reading
- Richardson, J.S. (1981). "Anatomy and Taxonomy of Protein Structures". Advances in Protein Chemistry. Advances in Protein Chemistry. 34: 167–339. doi:10.1016/S0065-3233(08)60520-3. ISBN 9780120342341. PMID 7020376., available on-line at Anatax
- Branden, C.-I.; Tooze, J. (1991), Introduction to Protein Structure, Garland Publishing, NY, ISBN 0-8153-0344-0
External links
| Wikimedia Commons has media related to Ramachandran plot. |
- DynoPlot in PyMOL wiki
- Link to Ramachandran Plot Map of alpha-helix and beta-sheet locations
- Link to Ramachandran plot calculated from protein structures determined by X-ray crystallography compared to the original Ramachan.
- Proteopedia Ramachandran Plot
