Sagitta (geometry)

Visualization of the sagitta

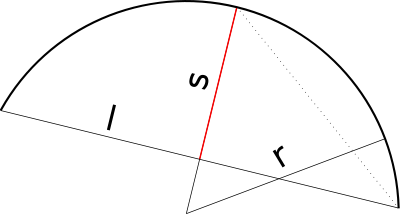
In geometry, the sagitta (sometimes abbreviated as sag^[1]) of a circular arc is the distance from the center of the arc to the center of its base.^[2] It is used extensively in architecture when calculating the arc necessary to span a certain height and distance and also in optics where it is used to find the depth of a spherical mirror or lens. The name comes directly from Latin sagitta, meaning an arrow.

Formulae

In the following equations, s denotes the sagitta (the depth of the arc), r equals the radius of the circle, and ℓ half the length of the chord spanning the base of the arc. As ℓ and r−s are two sides of a right triangle with r as the hypotenuse, the Pythagorean theorem gives us

${\displaystyle r^{2}=\ell ^{2}+(r-s)^{2}.}$

This may be rearranged to give any of the other three:

${\displaystyle s=r-{\sqrt {r^{2}-{\ell ^{2}}}},}$

${\displaystyle \ell ={\sqrt {2rs-s^{2}}},}$ or

${\displaystyle r={\frac {s^{2}+\ell ^{2}}{2s}}={\frac {s}{2}}+{\frac {\ell ^{2}}{2s}}.}$

The sagitta may also be calculated from the versine function, for an arc that spans an angle of Δ = 2θ, and coincides with the versine for unit circles

${\displaystyle s=r\operatorname {versin} \theta =r\left(1-\cos \theta \right)=2r\sin ^{2}{\frac {\theta }{2}}.}$

Approximation

When the sagitta is small in comparison to the radius, it may be approximated by the formula

$s\approx {\frac {\ell ^{2}}{2r}}$.^[2]

Alternatively, if the sagitta is small and the sagitta, radius, and half-chord length are known, they may be used to estimate the arc length by the formula

$a\approx \ell +{\frac {s^{2}}{r}}$,

where a is half the length of the arc; this formula was known to the Chinese mathematician Shen Kuo, and a more accurate formula also involving the sagitta was developed two centuries later by Guo Shoujing.^[3]

Applications

Architects, engineers, and contractors use these equations to create "flattened" arcs that are used in curved walls, arched ceilings, bridges, and numerous other applications.

The sagitta also has uses in physics where it is used, along with chord length, to calculate the radius of curvature of an accelerated particle. This is used especially in bubble chamber experiments where it is used to determine the momenta of decay particles.

See also

• Circular segment
• Versine

References

1. Shaneyfelt, Ted V. "德博士的 Notes About Circles, ज्य, & कोज्य: What in the world is a hacovercosine?". Hilo, Hawaii: University of Hawaii. Archived from the original on 2015-09-19. Retrieved 2015-11-08.
2. Woodward, Ernest (December 1978). Geometry - Plane, Solid & Analytic Problem Solver. Problem Solvers Solution Guides. Research & Education Association (REA). p. 359. ISBN 978-0-87891-510-1.
3. Needham, Noel Joseph Terence Montgomery (1959). Science and Civilisation in China: Mathematics and the Sciences of the Heavens and the Earth. 3. Cambridge University Press. p. 39. ISBN 9780521058018.

External links

• Calculating the Sagitta of an Arc