Singular control
In optimal control, problems of singular control are problems that are difficult to solve because a straightforward application of Pontryagin's minimum principle fails to yield a complete solution. Only a few such problems have been solved, such as Merton's portfolio problem in financial economics or trajectory optimization in aeronautics. A more technical explanation follows.
The most common difficulty in applying Pontryagin's principle arises when the Hamiltonian depends linearly on the control 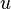 , i.e., is of the form:
, i.e., is of the form: 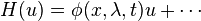 and the control is restricted to being between an upper and a lower bound:
and the control is restricted to being between an upper and a lower bound:  . To minimize
. To minimize 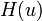 , we need to make
, we need to make 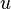 as big or as small as possible, depending on the sign of
as big or as small as possible, depending on the sign of 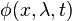 , specifically:
, specifically:
If 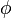 is positive at some times, negative at others and is only zero instantaneously, then the solution is straightforward and is a bang-bang control that switches from
is positive at some times, negative at others and is only zero instantaneously, then the solution is straightforward and is a bang-bang control that switches from 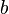 to
to 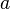 at times when
at times when 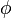 switches from negative to positive.
switches from negative to positive.
The case when 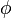 remains at zero for a finite length of time
remains at zero for a finite length of time  is called the singular control case. Between
is called the singular control case. Between 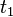 and
and 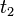 the maximization of the Hamiltonian with respect to u gives us no useful information and the solution in that time interval is going to have to be found from other considerations. (One approach would be to repeatedly differentiate
the maximization of the Hamiltonian with respect to u gives us no useful information and the solution in that time interval is going to have to be found from other considerations. (One approach would be to repeatedly differentiate 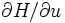 with respect to time until the control u again explicitly appears, which is guaranteed to happen eventually. One can then set that expression to zero and solve for u. This amounts to saying that between
with respect to time until the control u again explicitly appears, which is guaranteed to happen eventually. One can then set that expression to zero and solve for u. This amounts to saying that between 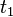 and
and 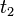 the control
the control 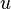 is determined by the requirement that the singularity condition continues to hold. The resulting so-called singular arc will be optimal if it satisfies the Kelley condition:
is determined by the requirement that the singularity condition continues to hold. The resulting so-called singular arc will be optimal if it satisfies the Kelley condition:
.[1] This condition is also called the generalized Legendre-Clebsch condition).
The term bang-singular control refers to a control that has a bang-bang portion as well as a singular portion.
References
- ↑ Bryson, Ho: Applied Optimal Control, Page 246
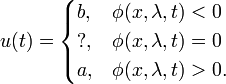
![(-1)^k \frac{\partial}{\partial u} \left[ {\left( \frac{d}{dt} \right)}^{2k} H_u \right] \ge 0 ,\, k=0,1,\cdots](../I/m/c82df4a816296ecad556ba3012732bc9.png)