Spin Hall effect

The Spin Hall Effect (SHE) is a transport phenomenon predicted by Russian physicists M.I. Dyakonov and V.I. Perel in 1971.[1][2] It consists of the appearance of spin accumulation on the lateral surfaces of an electric current-carrying sample, the signs of the spin directions being opposite on the opposing boundaries. In a cylindrical wire, the current-induced surface spins will wind around the wire. When the current direction is reversed, the directions of spin orientation is also reversed.

Schematic of the spin Hall effect
Schematic of the inverse spin Hall effect

Definition

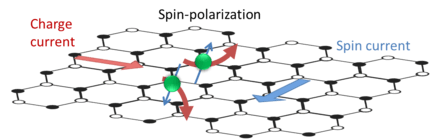
The Spin Hall Effect is a transport phenomenon consisting of the appearance of spin accumulation on the lateral surfaces of a sample carrying electric current. The opposing surface boundaries will have spins of opposite sign. It is analogous to the classical Hall effect, where charges of opposite sign appear on the opposing lateral surfaces in an electric-current carrying sample in a magnetic field. In the case of the classical Hall effect the charge build up at the boundaries is in compensation for the Lorentz force acting on the charge carriers in the sample due to the magnetic field. No magnetic field is needed for the SHE which is a purely spin-based phenomenon. The SHE belongs to the same family as the anomalous Hall effect, known for a long time in ferromagnets, which also originates from spin-orbit interaction.[3]

History

Predicted by Russian physicists M.I. Dyakonov and V.I. Perel in 1971.[1][2]

The term "Spin Hall Effect" was introduced by Jorge Hirsch[4] in 1999. Unaware of the work of Dyakonov and Perel, Hirsch used subtle physical reasoning based on the anomalous Hall effect to predict both the SHE and the inverse SHE. Averkiev and Dyakonov had earlier predicted the SHE [N.S. Averkiev and M.I. Dyakonov, JETP Lett. 35, 196 (1983)], and it had been observed [A.A. Bakun et al., JETP Lett. 40, 1293 (1984)].

Experimentally, the Spin Hall Effect was observed in semiconductors [5][6] more than 30 years after the original prediction.

Properties

The origin of SHE is in the spin-orbit interaction, which leads to the coupling of spin and charge currents: an electric current induces a transverse spin current (a flow of spins), which, in turn, leads to an accumulation of spins of opposite signs on opposing lateral boundaries.[1][2][7] One can intuitively understand this effect by using the analogy between an electron and a spinning tennis ball, which deviates from its straight path in air in a direction depending on the sense of rotation (the Magnus effect).

Interaction With Magnetic Fields

No magnetic field is needed for SHE. However, if a strong enough magnetic field is applied in the direction perpendicular to the orientation of the spins at the surfaces, spins will precess around the direction of the magnetic field and the SHE will disappear.[2][7]

Optics

The SHE can be monitored by optical means. The spin accumulation induces circular polarization of the emitted light, as well as the Faraday (or Kerr) polarization rotation of the transmitted (or reflected) light. Observing the polarization of emitted light allows the SHE to be observed.

Inverse Spin-Hall Effect

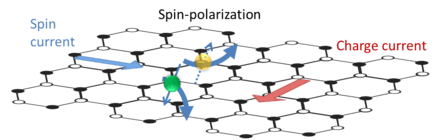
For the Inverse Spin Hall Effect a space-dependent spin-polarization causes a spin-polarized current which induces an electric current which leads to an accumulation of electrical charges of opposite signs on opposing lateral boundaries. This can be measured as a charge imbalance at the edges of the sample. It was first observed in 1984.[8] More recently, the existence of both direct and inverse effects was demonstrated not only in semiconductors,[9] but also in metals.[10][11][12]

Applications

The SHE can be used to manipulate electron spins electrically. For example, in combination with the electric stirring effect, the SHE leads to spin polarization in a localized conducting region.[13]

References

  1. 1 2 3 M. I. Dyakonov and V. I. Perel,; Perel' (1971). "Possibility of orientating electron spins with current". Sov. Phys. JETP Lett. 13: 467. Bibcode:1971JETPL..13..467D.
  2. 1 2 3 4 M.I. Dyakonov & V.I. Perel (1971). "Current-induced spin orientation of electrons in semiconductors". Phys. Lett. A. 35 (6): 459. Bibcode:1971PhLA...35..459D. doi:10.1016/0375-9601(71)90196-4.
  3. ↑ N.A. Sinitsyn (2008). "Semiclassical Theories of the Anomalous Hall Effect". J. Phys.: Condens. Matter. 20 (2): 023201. arXiv:0712.0183Freely accessible. Bibcode:2008JPCM...20b3201S. doi:10.1088/0953-8984/20/02/023201.
  4. ↑ J.E. Hirsch (1999). "Spin Hall Effect" (subscription required). Phys. Rev. Lett. 83 (9): 1834. arXiv:cond-mat/9906160Freely accessible. Bibcode:1999PhRvL..83.1834H. doi:10.1103/PhysRevLett.83.1834.
  5. ↑ Y. Kato; R. C. Myers; A. C. Gossard; D. D. Awschalom (11 November 2004). "Observation of the Spin Hall Effect in Semiconductors". Science. 306 (5703): 1910–1913. Bibcode:2004Sci...306.1910K. doi:10.1126/science.1105514. PMID 15539563.
  6. ↑ J. Wunderlich; B. Kaestner; J. Sinova; T. Jungwirth (2005). "Experimental Observation of the Spin-Hall Effect in a Two-DimensionalSpin-Orbit Coupled Semiconductor System". Phys. Rev. Lett. 94 (4): 047204. arXiv:cond-mat/0410295Freely accessible. Bibcode:2005PhRvL..94d7204W. doi:10.1103/PhysRevLett.94.047204. PMID 15783592.
  7. 1 2 M.I. Dyakonov (2007). "Magnetoresistance due to edge spin accumulation" (abstract page). Phys. Rev. Lett. 99 (12): 126601. arXiv:0705.2738Freely accessible. Bibcode:2007PhRvL..99l6601D. doi:10.1103/PhysRevLett.99.126601. PMID 17930533.
  8. ↑ A.A. Bakun; B.P. Zakharchenya; A.A. Rogachev; M.N. Tkachuk; V.G. Fleisher (1984). "Detection of a surface photocurrent due to electron optical orientation in a semiconductor". Sov. Phys. JETP Lett. 40: 1293. Bibcode:1984JETPL..40.1293B.
  9. ↑ H. Zhao; E. J. Loren; H. M. van Driel; A. L. Smirl (2006). "Coherence Control of Hall Charge and Spin Currents". Phys. Rev. Lett. 96 (24): 246601. Bibcode:2006PhRvL..96x6601Z. doi:10.1103/PhysRevLett.96.246601. PMID 16907264.
  10. ↑ E. Saitoh; M Ueda; H. Miyajima; G. Tatara (2006). "Conversion of spin current into charge current at room temperature: inverse spin-Hall effect". Applied Physics Letters. 88 (18): 182509. Bibcode:2006ApPhL..88r2509S. doi:10.1063/1.2199473.
  11. ↑ S.O. Valenzuela; M. Tinkham (2006). "Direct Electronic Measurement of the Spin Hall Effect". Nature. 442 (7099): 176–9. arXiv:cond-mat/0605423Freely accessible. Bibcode:2006Natur.442..176V. doi:10.1038/nature04937. PMID 16838016.
  12. ↑ T. Kimura; Y. Otani; T. Sato; S. Takahashi; S. Maekawa (2007). "Room-Temperature Reversible Spin Hall Effect". Phys. Rev. Lett. 98 (15): 156601. arXiv:cond-mat/0609304Freely accessible. Bibcode:2007PhRvL..98o6601K. doi:10.1103/PhysRevLett.98.156601. PMID 17501368.
  13. ↑ Yu. V. Pershin, N.A. Sinitsyn, A. Kogan, A. Saxena and D. Smith (2009). "Spin polarization control by electric stirring: proposal for a spintronic device". Appl. Phys. Lett. 95 (2): 022114. arXiv:0906.0039Freely accessible. Bibcode:2009ApPhL..95b2114P. doi:10.1063/1.3180494.
This article is issued from Wikipedia - version of the 6/17/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.