Star of David theorem
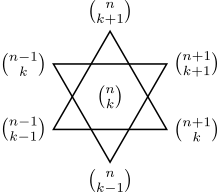
The Star of David theorem (the rows of the Pascal triangle are shown as columns here).
The Star of David theorem is a mathematical result on arithmetic properties of binomial coefficients. It was discovered by Henry W. Gould in 1972.
Statement
The greatest common divisors of binomial coefficients forming the Star of David shape in Pascal's triangle, are equal:
See also
References
- H.W. Gould, A New Greatest Common Divisor Property of The Binomial Coefficients, Fibonacci Quarterly 10 (1972), 579–584.
- Star of David theorem, from MathForum.
- Star of David theorem, blog post.
External links
This article is issued from Wikipedia - version of the 4/9/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
![\begin{align}
& {} \quad \gcd\left\{ \binom{n-1}{k-1}, \binom{n}{k+1}, \binom{n+1}{k}\right\} \\[8pt]
& = \gcd\left\{ \binom{n-1}{k}, \binom{n}{k-1}, \binom{n+1}{k+1}\right\}.
\end{align}](../I/m/01d7b3bc539e33888f5804160b66af50.png)