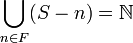Syndetic set
In mathematics, a syndetic set is a subset of the natural numbers, having the property of "bounded gaps": that the sizes of the gaps in the sequence of natural numbers is bounded.
Definition
A set 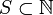 is called syndetic if for some finite subset F of
is called syndetic if for some finite subset F of 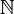
where 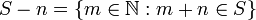 . Thus syndetic sets have "bounded gaps"; for a syndetic set
. Thus syndetic sets have "bounded gaps"; for a syndetic set 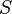 , there is an integer
, there is an integer 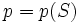 such that
such that ![[a, a+1, a+2, ... , a+p] \bigcap S \neq \emptyset](../I/m/874f98e06e2e5e3ec24a77862aab9c97.png) for any
for any 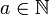 .
.
See also
References
- J. McLeod, "Some Notions of Size in Partial Semigroups", Topology Proceedings, Vol. 25 (2000), pp. 317-332
- Vitaly Bergelson, "Minimal Idempotents and Ergodic Ramsey Theory", Topics in Dynamics and Ergodic Theory 8-39, London Math. Soc. Lecture Note Series 310, Cambridge Univ. Press, Cambridge, (2003)
- Vitaly Bergelson, N. Hindman, "Partition regular structures contained in large sets are abundant", J. Comb. Theory (Series A) 93 (2001), pp. 18-36
This article is issued from Wikipedia - version of the 12/27/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.