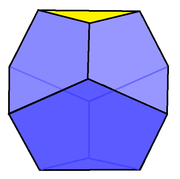
Truncated triangular trapezohedron
| Truncated triangular trapezohedron Dürer's solid | |
|---|---|
 | |
| Type | Truncated trapezohedron |
| Faces | 6 pentagons, 2 triangles |
| Edges | 18 |
| Vertices | 12 |
| Symmetry group | D3d, [2+,6], (2*3) |
| Dual polyhedron | Gyroelongated triangular dipyramid |
| Properties | convex |
In geometry, the truncated triangular trapezohedron is the first in an infinite series of truncated trapezohedron polyhedra. It has 6 pentagon and 2 triangle faces.
Geometry
This polyhedron can be constructed by truncating two opposite vertices of a cube, of a trigonal trapezohedron (a convex polyhedron with six congruent rhombus sides, formed by stretching or shrinking a cube along one of its long diagonals), or of a rhombohedron or parallelepiped (less symmetric polyhedra that still have the same combinatorial structure as a cube). In the case of a cube, or of a trigonal trapezohedron where the two truncated vertices are the ones on the stretching axes, the resulting shape has three-fold rotational symmetry.
Dürer's solid

This polyhedron is sometimes called Dürer's solid, from its appearance in Albrecht Dürer's 1514 engraving Melencolia I. The graph formed by its edges and vertices is called the Dürer graph.
The shape of the solid depicted by Dürer is a subject of some academic debate.[1] According to Lynch (1982), the hypothesis that the shape is a misdrawn truncated cube was promoted by Strauss (1972); however most sources agree that it is the truncation of a rhombohedron. Despite this agreement, the exact geometry of this rhombohedron is the subject of several contradictory theories:
- Richter (1957) claims that the rhombi of the rhombohedron from which this shape is formed have 5:6 as the ratio between their short and long diagonals, from which the acute angles of the rhombi would be approximately 80°.
- Schröder (1980) and Lynch (1982) instead conclude that the ratio is √3:2 and that the angle is approximately 82°.
- MacGillavry (1981) measures features of the drawing and finds that the angle is approximately 79°. He and a later author, Wolf von Engelhardt (see Hideko 2009) argue that this choice of angle comes from its physical occurrence in calcite crystals.
- Schreiber (1999) argues based on the writings of Dürer that all vertices of Dürer's solid lie on a common sphere, and further claims that the rhombus angles are 72°. Hideko (2009) lists several other scholars who also favor the 72° theory, beginning with Paul Grodzinski in 1955. He argues that this theory is motivated less by analysis of the actual drawing, and more by aesthetic principles relating to regular pentagons and the golden ratio.
- Weitzel (2004) analyzes a 1510 sketch by Dürer of the same solid, from which he confirms Schreiber's hypothesis that the shape has a circumsphere but with rhombus angles of approximately 79.5°.
- Hideko (2009) argues that the shape is intended to depict a solution to the famous geometric problem of doubling the cube, which Dürer also wrote about in 1525. He therefore concludes that (before the corners are cut off) the shape is a cube stretched along its long diagonal. More specifically, he argues that Dürer drew an actual cube, with the long diagonal parallel to the perspective plane, and then enlarged his drawing by some factor in the direction of the long diagonal; the result would be the same as if he had drawn the elongated solid. The enlargement factor that is relevant for doubling the cube is 21/3 ≈ 1.253, but Hideko derives a different enlargement factor that fits the drawing better, 1.277, in a more complicated way.
- Futamura, Frantz & Crannell (2014) classify the proposed solutions to this problem by two parameters: the acute angle and the level of cutting, called the cross ratio. Their estimate of the cross ratio is close to MacGillavry's, and has a numerical value close to the golden ratio. Based on this they posit that the acute angle is and that the cross ratio is exactly .
See also
- Chamfered tetrahedron, another shape formed by truncating a subset of the vertices of a cube
Notes
- ↑ See Weitzel (2004) and Ziegler (2014), from which much of the following history is drawn.
References
- Lynch, Terence (1982), "The geometric body in Dürer's engraving Melencolia I", Journal of the Warburg and Courtauld Institutes, The Warburg Institute, 45: 226–232, doi:10.2307/750979, JSTOR 750979.
- MacGillavry, C. (1981), "The polyhedron in A. Dürers Melencolia I", Nederl. Akad. Wetensch. Proc. Ser. B, 84: 287–294. As cited by Weitzel (2004).
- Richter, D. H. (1957), "Perspektive und Proportionen in Albrecht Dürers "Melancholie"", Z. Vermessungswesen, 82: 284–288 and 350–357. As cited by Weitzel (2004).
- Schreiber, Peter (1999), "A new hypothesis on Dürer's enigmatic polyhedron in his copper engraving "Melencolia I"", Historia Mathematica, 26: 369–377, doi:10.1006/hmat.1999.2245.
- Schröder, E. (1980), Dürer, Kunst und Geometrie, Dürers künstlerisches Schaffen aus der Sicht seiner "Underweysung", Basel. As cited by Weitzel (2004).
- Strauss, Walter L. (1972), The Complete Engravings of Dürer, New York, p. 168, ISBN 0-486-22851-7. As cited by Lynch (1982).
- Weber, P. (1900), Beiträge zu Dürers Weltanschauung—Eine Studie über die drei Stiche Ritter, Tod und Teufel, Melancholie und Hieronymus im Gehäus, Strassburg. As cited by Weitzel (2004).
- Weitzel, Hans (2004), "A further hypothesis on the polyhedron of A. Dürer's engraving Melencolia I", Historia Mathematica, 31 (1): 11–14, doi:10.1016/S0315-0860(03)00029-6.
- Hideko, Ishizu (2009), "Another solution to the polyhedron in Dürer's Melencolia: A visual demonstration of the Delian problem" (PDF), Aesthetics, The Japanese Society for Aesthetics, 13: 179–194.
- Ziegler, Günter M. (December 3, 2014), "Dürer's polyhedron: 5 theories that explain Melencolia's crazy cube", Alex Bellos's Adventures in Numberland, The Guardian.
- Futamura, F.; Frantz, M.; Crannell, A. (2014), "The cross ratio as a shape parameter for Dürer's solid", Journal of Mathematics and the Arts, 8 (3-4): 111–119, arXiv:1405.6481
 , doi:10.1080/17513472.2014.974483.
, doi:10.1080/17513472.2014.974483.