Vector-radix FFT algorithm

The vector-radix FFT algorithm, is a multidimensional fast Fourier transform (FFT) algorithm, which is a generalization of the ordinary Cooley–Tukey FFT algorithm that divides the transform dimensions by arbitrary radices. It breaks a multidimensional (MD) discrete Fourier transform (DFT) down into successively smaller MD DFTs until, ultimately, only trivial MD DFTs need to be evaluated.^[1]
The most common multidimensional FFT algorithm is row-column algorithm, which means transforming the array first in one index and then in the other, see more in FFT. Then a radix-2 direct 2-D FFT has been developed,^[2] and it can eliminate 25% of the multiplies by the conventional row-column approach. And this algorithm has been extended to rectangular arrays and arbitrary radices,^[3] which is the general Vector-Radix algorithm. Perhaps it is the simplest non-row-column FFT algorithm.
Vector-radix FFT algorithm can reduce the number of complex multiplications significantly, compared to row-vector algorithm. For example, for a ${\displaystyle N^{M}}$ time matrix (M dimensions, and size N on each dimension), the number of complex multiples of vector-radix FFT algorithm is ${\displaystyle {\frac {2^{M}-1}{2^{M}}}N^{M}\log _{2}N}$, meanwhile, for row-column algorithm, it is ${\displaystyle {\frac {MN^{M}}{2}}\log _{2}N}$. And generally, even larger savings in multiplies are obtained when this algorithm is operated on larger radices and on higher dimensional arrays.^[3]

2-D DIT case

As with Cooley–Tukey FFT algorithm, two dimensional vector-radix FFT is derived by decomposing the regular 2-D DFT into sums of smaller DFT's multiplied by "twiddle" factor.
A decimation-in-time (DIT) algorithm means the decomposition is based on time domain $x$, see more in Cooley–Tukey FFT algorithm.

We suppose the 2-D DFT

${\displaystyle X(k_{1},k_{2})=\sum _{n_{1}=0}^{N_{1}-1}\sum _{n_{2}=0}^{N_{2}-1}x[n_{1},n_{2}]\cdot W_{N_{1}}^{k_{1}n_{1}}W_{N_{2}}^{k_{2}n_{2}},}$

where ${\displaystyle k_{1}=0,\dots ,N_{1}-1}$,and ${\displaystyle k_{2}=0,\dots ,N_{2}-1}$, and ${\displaystyle x[n_{1},n_{2}]}$ is a ${\displaystyle N_{1}\times N_{2}}$ matrix, and ${\displaystyle W_{N}^{kn}=\exp(-j2\pi /N)}$.

For simplicity, let us assume that ${\displaystyle N_{1}=N_{2}=N}$, and radix-$(r\times r)$(${\displaystyle N/r}$ are integers).

Using the change of variables:

• ${\displaystyle n_{i}=rp_{i}+q_{i}}$, where ${\displaystyle p_{i}=0,\ldots ,(N/r)-1;q_{i}=0,\ldots ,r-1;}$
• ${\displaystyle k_{i}=u_{i}+v_{i}N/r}$, where ${\displaystyle u_{i}=0,\ldots ,(N/r)-1;v_{i}=0,\ldots ,r-1;}$

where $i=1$ or $2$.

Then, the two dimensional DFT can be written as:

${\displaystyle X(u_{1}+v_{1}N/r,u_{2}+v_{2}N/r)=\sum _{q_{1}=0}^{r-1}\sum _{q_{2}=0}^{r-1}\left[\sum _{p_{1}=0}^{N/r-1}\sum _{p_{2}=0}^{N/r-1}x[rp_{1}+q_{1},rp_{1}+q_{1}]W_{N/r}^{p_{1}u_{1}}W_{N/r}^{p_{2}u_{2}}\right]\cdot W_{N}^{q_{1}u_{1}+q_{2}u_{2}}W_{r}^{q_{1}v_{1}}W_{r}^{q_{2}v_{2}},}$

One stage "butterfly" for DIT vector-radix 2x2 FFT

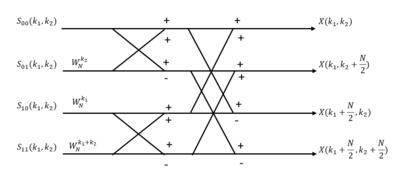
The equation above defines the basic structure of the 2-D DIT radix-$(r\times r)$ "butterfly". (See 1-D "butterfly" in Cooley–Tukey FFT algorithm)

When $r=2$, the equation can be broken into four summations: one over those samples of x for which both $n_{1}$ and $n_{2}$ are even, one for which $n_{1}$ is even and $n_{2}$ is odd, one of which $n_{1}$ is odd and $n_{2}$ is even, and one for which both $n_{1}$ and $n_{2}$ are odd,^[1] and this leads to:

${\displaystyle X(k_{1},k_{2})=S_{00}(k_{1},k_{2})+S_{01}(k_{1},k_{2})W_{N}^{k_{2}}+S_{10}(k_{1},k_{2})W_{N}^{k_{1}}+S_{11}(k_{1},k_{2})W_{N}^{k_{1}+k_{2}},}$

where ${\displaystyle S_{ij}(k_{1},k_{2})=\sum _{n_{1}=0}^{N/2-1}\sum _{n_{2}=0}^{N/2-1}x[2n_{1}+i,2n_{2}+j]\cdot W_{N/2}^{n_{1}k_{1}}W_{N/2}^{n_{2}k_{2}}.}$

2-D DIF case

Similarly, a decimation-in-frequency (DIF, also called the Sande-Tukey algorithm) algorithm means the decomposition is based on frequency domain $X$, see more in Cooley–Tukey FFT algorithm.

Using the change of variables:

• ${\displaystyle n_{i}=p_{i}+q_{i}N/r}$, where ${\displaystyle p_{i}=0,\ldots ,(N/r)-1;q_{i}=0,\ldots ,r-1;}$
• ${\displaystyle k_{i}=ru_{i}+v_{i}}$, where ${\displaystyle u_{i}=0,\ldots ,(N/r)-1;v_{i}=0,\ldots ,r-1;}$

where $i=1$ or $2$.

And the DFT equation can be written as:

${\displaystyle X(ru_{1}+v_{1},ru_{2}+v_{2})=\sum _{p_{1}=0}^{N/r-1}\sum _{p_{2}=0}^{N/r-1}\left[\sum _{q_{1}=0}^{r-1}\sum _{q_{2}=0}^{r-1}x[p_{1}+q_{1}N/r,p_{1}+q_{1}N/r]W_{r}^{q_{1}v_{1}}W_{r}^{q_{2}v_{2}}\right]\cdot W_{N}^{p_{1}v_{1}+p_{2}v_{2}}W_{N/r}^{p_{1}u_{1}}W_{N/r}^{p_{2}u_{2}},}$

Other approaches

The Split-radix FFT algorithm has been proved to be a useful method for 1-D DFT. And this method has been applied to the vector-radix FFT to obtain a split vector-radix FFT.^[4][5]

In conventional 2-D vector-radix algorithm, we decompose the incident $k_{1},k_{2}$ into 4 groups:

${\displaystyle {\begin{array}{lcl}X(2k_{1},2k_{2})&:&{\text{even-even}}\\X(2k_{1},2k_{2}+1)&:&{\text{even-odd}}\\X(2k_{1}+1,2k_{2})&:&{\text{odd-even}}\\X(2k_{1}+1,2k_{2}+1)&:&{\text{odd-odd}}\end{array}}}$

By the split vector-radix algorithm, the first three groups remain unchanged, the fourth odd-odd group is further decomposed into another four sub-groups, and seven groups in total:

${\displaystyle {\begin{array}{lcl}X(2k_{1},2k_{2})&:&{\text{even-even}}\\X(2k_{1},2k_{2}+1)&:&{\text{even-odd}}\\X(2k_{1}+1,2k_{2})&:&{\text{odd-even}}\\X(4k_{1}+1,4k_{2}+1)&:&{\text{odd-odd}}\\X(4k_{1}+1,4k_{2}+3)&:&{\text{odd-odd}}\\X(4k_{1}+3,4k_{2}+1)&:&{\text{odd-odd}}\\X(4k_{1}+3,4k_{2}+3)&:&{\text{odd-odd}}\end{array}}}$

That means the fourth term in 2-D DIT radix-${\displaystyle (2\times 2)}$ equation, ${\displaystyle S_{11}(k_{1},k_{2})W_{N}^{k_{1}+k_{2}}}$ becomes:

${\displaystyle A_{11}(k_{1},k_{2})W_{N}^{k_{1}+k_{2}}+A_{13}(k_{1},k_{2})W_{N}^{k_{1}+3k_{2}}+A_{31}(k_{1},k_{2})W_{N}^{3k_{1}+k_{2}}+A_{33}(k_{1},k_{2})W_{N}^{3(k_{1}+k_{2})},}$

where ${\displaystyle A_{ij}(k_{1},k_{2})=\sum _{n_{1}=0}^{N/4-1}\sum _{n_{2}=0}^{N/4-1}x[4n_{1}+i,4n_{2}+j]\cdot W_{N/4}^{n_{1}k_{1}}W_{N/4}^{n_{2}k_{2}}}$

The 2-D N by N DFT is then obtained by successive use of the above decomposition, up to the last stage.
It has been shown that the split vector radix algorithm has saved about 30% of the complex multiplications and about the same number of the complex additions for typical ${\displaystyle 1024\times 1024}$ array, compared with the vector-radix algorithm.^[4]

References

1. Dudgeon, Dan; Russell, Mersereau (September 1983). Multidimensional Digital Signal Processing. Prentice Hall. p. 76. ISBN 0136049591.
2. Rivard, G. "Direct fast Fourier transform of bivariate functions". IEEE Transactions on Acoustics, Speech, and Signal Processing. 25: 250–252. doi:10.1109/TASSP.1977.1162951.
3. Harris, D.; McClellan, J.; Chan, D.; Schuessler, H. "Vector radix fast Fourier transform". Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP '77. 2: 548–551. doi:10.1109/ICASSP.1977.1170349.
4. Pei, Soo-Chang; Wu, Ja-Lin (April 1987). "Split vector radix 2D fast Fourier transform". Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP '87.: 1987–1990. doi:10.1109/ICASSP.1987.1169345.
5. Chan, S. C.; Ho, K. L. "Split vector-radix fast Fourier transform". IEEE Transactions on Signal Processing. 40: 2029–2039. doi:10.1109/78.150004.