Waves in plasmas
In plasma physics, waves in plasmas are an interconnected set of particles and fields which propagates in a periodically repeating fashion. A plasma is a quasineutral, electrically conductive fluid. In the simplest case, it is composed of electrons and a single species of positive ions, but it may also contain multiple ion species including negative ions as well as neutral particles. Due to its electrical conductivity, a plasma couples to electric and magnetic fields. This complex of particles and fields supports a wide variety of wave phenomena.
Terminology and classification
Waves in plasmas can be classified as electromagnetic or electrostatic according to whether or not there is an oscillating magnetic field. Applying Faraday's law of induction to plane waves, we find 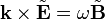 , implying that an electrostatic wave must be purely longitudinal. An electromagnetic wave, in contrast, must have a transverse component, but may also be partially longitudinal.
, implying that an electrostatic wave must be purely longitudinal. An electromagnetic wave, in contrast, must have a transverse component, but may also be partially longitudinal.
Waves can be further classified by the oscillating species. In most plasmas of interest, the electron temperature is comparable to or larger than the ion temperature. This fact, coupled with the much smaller mass of the electron, implies that the electrons move much faster than the ions. An electron mode depends on the mass of the electrons, but the ions may be assumed to be infinitely massive, i.e. stationary. An ion mode depends on the ion mass, but the electrons are assumed to be massless and to redistribute themselves instantaneously according to the Boltzmann relation. Only rarely, e.g. in the lower hybrid oscillation, will a mode depend on both the electron and the ion mass.
The various modes can also be classified according to whether they propagate in an unmagnetized plasma or parallel, perpendicular, or oblique to the stationary magnetic field. Finally, for perpendicular electromagnetic electron waves, the perturbed electric field can be parallel or perpendicular to the stationary magnetic field.
| EM character | oscillating species | conditions | dispersion relation | name |
|---|---|---|---|---|
| electrostatic | electrons | 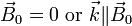 | 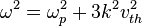 | plasma oscillation (or Langmuir wave) |
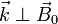 | 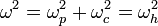 | upper hybrid oscillation | ||
| ions | 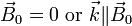 | 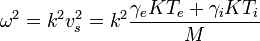 | ion acoustic wave | |
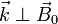 (nearly) (nearly) | 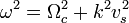 | electrostatic ion cyclotron wave | ||
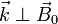 (exactly) (exactly) | ![\omega^2=[(\Omega_c\omega_c)^{-1}+\omega_i^{-2}]^{-1}](../I/m/6f31c7faf14ac9eba6788f9e038fdc3a.png) | lower hybrid oscillation | ||
| electromagnetic | electrons | 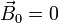 | 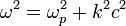 | light wave |
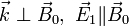 | 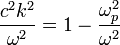 | O wave | ||
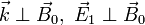 | 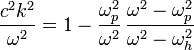 | X wave | ||
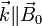 (right circ. pol.) (right circ. pol.) | 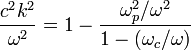 | R wave (whistler mode) | ||
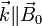 (left circ. pol.) (left circ. pol.) | 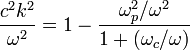 | L wave | ||
| ions | 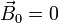 | none | ||
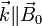 | 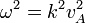 | Alfvén wave | ||
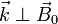 | 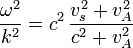 | magnetosonic wave |
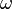 - wave frequency,
- wave frequency,
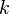 - wave number,
- wave number,
 - speed of light,
- speed of light,
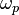 - plasma frequency,
- plasma frequency,
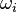 - ion plasma frequency,
- ion plasma frequency,
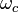 - electron gyrofrequency,
- electron gyrofrequency,
 - proton gyrofrequency,
- proton gyrofrequency,
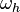 - upper hybrid frequency,
- upper hybrid frequency,
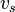 - plasma "sound" speed,
- plasma "sound" speed,
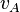 - plasma Alfvén speed
- plasma Alfvén speed
References
- Swanson, D.G. Plasma Waves (2003). 2nd edition.
- Stix, Thomas Howard. Waves in Plasmas (1992).
See also
- Magnetohydrodynamic waves
- Appleton-Hartree equation
- plasmon
- Surface plasmon resonance
- index of wave articles
- List of plasma (physics) applications articles