Weight (strings)
The 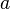 -weight of a string, for
-weight of a string, for 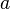 a letter, is the number of times that letter occurs in the string. More precisely, let
a letter, is the number of times that letter occurs in the string. More precisely, let 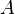 be a finite set (called the alphabet),
be a finite set (called the alphabet),  a letter of
a letter of 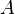 , and
, and  a
string (where
a
string (where 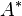 is the free monoid generated by the elements of
is the free monoid generated by the elements of 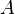 , equivalently the set of strings, including the empty string, whose letters are from
, equivalently the set of strings, including the empty string, whose letters are from 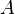 ). Then the
). Then the 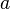 -weight of
-weight of  , denoted by
, denoted by  , is the number of times the generator
, is the number of times the generator 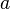 occurs in the unique expression for
occurs in the unique expression for  as a product (concatenation) of letters in
as a product (concatenation) of letters in 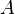 .
.
If 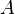 is an abelian group, the Hamming weight
is an abelian group, the Hamming weight  of
of  ,
often simply referred to as "weight", is the number of nonzero letters in
,
often simply referred to as "weight", is the number of nonzero letters in  .
.
Examples
- Let
 . In the string
. In the string  ,
, 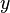 occurs 5 times, so the
occurs 5 times, so the 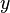 -weight of
-weight of  is
is  .
. - Let
 (an abelian group) and
(an abelian group) and  . Then
. Then  ,
,  ,
,  and
and  .
.
This article incorporates material from Weight (strings) on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.