Whitehead's lemma (Lie algebras)

In algebra, Whitehead's lemma on a Lie algebra representation is an important step toward the proof of Weyl's theorem on complete reducibility. Let 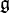$\mathfrak{g}$ be a semisimple Lie algebra over a field of characteristic zero, V a finite-dimensional module over it and 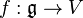$f: \mathfrak{g} \to V$ a linear map such that $f([x, y]) = xf(y) - yf(x)$. 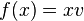The lemma states that there exists a vector v in V such that $f(x) = xv$ for all x.

The lemma may be interpreted in terms of Lie algebra cohomology. The proof of the lemma uses a Casimir element.

References

• Jacobson, Nathan, Lie algebras, Republication of the 1962 original. Dover Publications, Inc., New York, 1979. ISBN 0-486-63832-4