1/2 − 1/4 + 1/8 − 1/16 + ⋯

In mathematics, the infinite series 1/2 − 1/4 + 1/8 − 1/16 + ⋯ is a simple example of an alternating series that converges absolutely.

It is a geometric series whose first term is 1/2 and whose common ratio is −1/2, so its sum is

${\displaystyle {\frac {1}{2}}-{\frac {1}{4}}+{\frac {1}{8}}-{\frac {1}{16}}+\cdots ={\frac {\frac {1}{2}}{1-(-{\frac {1}{2}})}}={\frac {1}{3}}.}$

Hackenbush and the surreals

A slight rearrangement of the series reads

$1-{\frac 12}-{\frac 14}+{\frac 18}-{\frac {1}{16}}+\cdots ={\frac 13}.$

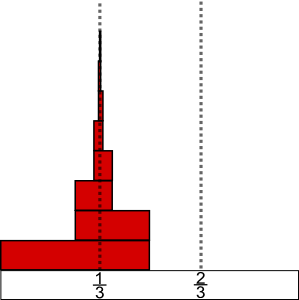
The series has the form of a positive integer plus a series containing every negative power of two with either a positive or negative sign, so it can be translated into the infinite blue-red Hackenbush string that represents the surreal number 1/3:

LRRLRLR… = 1/3.^[1]

A slightly simpler Hackenbush string eliminates the repeated R:

LRLRLRL… = 2/3.^[2]

In terms of the Hackenbush game structure, this equation means that the board depicted on the right has a value of 0; whichever player moves second has a winning strategy.

Related series

• The statement that 1/2 − 1/4 + 1/8 − 1/16 + ⋯ is absolutely convergent means that the series 1/2 + 1/4 + 1/8 + 1/16 + ⋯ is convergent. In fact, the latter series converges to 1, and it proves that one of the binary expansions of 1 is 0.111….
• Pairing up the terms of the series 1/2 − 1/4 + 1/8 − 1/16 + ⋯ results in another geometric series with the same sum, 1/4 + 1/16 + 1/64 + 1/256 + ⋯. This series is one of the first to be summed in the history of mathematics; it was used by Archimedes circa 250–200 BC.^[3]
• The Euler transform of the divergent series 1 − 2 + 4 − 8 + ⋯ is 1/2 − 1/4 + 1/8 − 1/16 + ⋯. Therefore, even though the former series does not have a sum in the usual sense, it is Euler summable to 1/3.^[4]

Notes

1. Berkelamp et al. p. 79
2. Berkelamp et al. pp. 307–308
3. Shawyer and Watson p. 3
4. Korevaar p. 325

References

• Berlekamp, E. R.; Conway, J. H.; Guy, R. K. (1982). Winning Ways for your Mathematical Plays. Academic Press. ISBN 0-12-091101-9.
• Korevaar, Jacob (2004). Tauberian Theory: A Century of Developments. Springer. ISBN 3-540-21058-X.
• Shawyer, Bruce; Watson, Bruce (1994). Borel's Methods of Summability: Theory and Applications. Oxford UP. ISBN 0-19-853585-6.