Auxetics

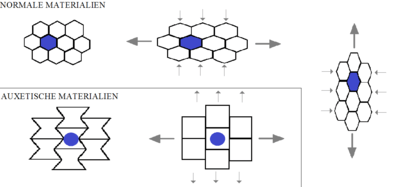
Auxetics are structures or materials that have a negative Poisson's ratio. When stretched, they become thicker perpendicular to the applied force. This occurs due to their particular internal structure and the way this deforms when the sample is uniaxially loaded. Auxetics can be single molecules, crystals, or a particular structure of macroscopic matter. Such materials and structures are expected to have mechanical properties such as high energy absorption and fracture resistance. Auxetics may be useful in applications such as body armor,^[1] packing material, knee and elbow pads, robust shock absorbing material, and sponge mops.

The term auxetic derives from the Greek word αὐξητικός (auxetikos) which means "that which tends to increase" and has its root in the word αὔξησις, or auxesis, meaning "increase" (noun). This terminology was coined by Professor Ken Evans of the University of Exeter.^[2]

The earliest published example of a synthetic auxetic material was in Science in 1987, entitled "Foam structures with a Negative Poisson's Ratio" ^[3] by R.S. Lakes from the University of Iowa. The use of the word auxetic to refer to this property probably began in 1991.^[4]

Designs of composites with inverted hexagonal periodicity cell (auxetic hexagon), possessing negative Poisson ratios, were published in 1985.^{[5][6][7][8][9][10]}

Typically, auxetic materials have low density, which is what allows the hinge-like areas of the auxetic microstructures to flex.^[11]

At the macroscale, auxetic behaviour can be illustrated with an inelastic string wound around an elastic cord. When the ends of the structure are pulled apart, the inelastic string straightens while the elastic cord stretches and winds around it, increasing the structure's effective volume.

Examples of auxetic materials include:

• Auxetic polyurethane foam^[12][13]
• Certain rocks and minerals^[14]
• Graphene, which can be made auxetic through the introduction of vacancy defects^[15]
• Living bone tissue (although this is only suspected)^[14]
• Tendons within their normal range of motion.^[16]
• Specific variants of polytetrafluorethylene polymers such as Gore-Tex^[17]
• Paper, all types. If a paper is stretched in an in-plane direction it will expand in its thickness direction due to its network structure.^[18][19]
• Several types of origami folds such as the miura fold,^[20][21] and other periodic patterns derived from it.^[22]
• Tailored structures designed to exhibit special designed Poisson's ratios.^[23]
• Chain organic molecules. Recent researches revealed that organic crystals like n-paraffins and similar to them may demonstrate an auxetic behavior.^[24]
• Processed needle-punched nonwoven fabrics. Due to the network structure of such fabrics, a processing protocol using heat and pressure can convert ordinary (not auxetic) nonwovens into auxetic ones.^[25]

Tomb towers of two Seljuk princes at Kharaghan, Qazvin province, Iran, covered with many different brick patterns like those that inspired Ahmad Rafsanjani to create auxetic materials

In footwear, auxetic design allows the sole to expand in size while walking or running, thereby increasing flexibility.

In 2016, Ahmad Rafsanjani described the use of Islamic geometric patterns from tomb towers in Iran to create auxetic materials from perforated rubber sheets. These are stable in either a contracted or an expanded state, and can switch between the two. The internal structure that enables this unusual behaviour is inspired by two of the 70 Islamic patterns that Rafsanjani noted on the tomb towers.^[26]

See also

• Acoustic metamaterials
• Mechanical metamaterials
• Metamaterials
• Zetix, a type of commercially manufactured auxetic material

References

1. "Hook's law". The Economist. 1 December 2012. Retrieved 1 March 2013.
2. Quinion, Michael (1996-11-09), Auxetic, retrieved 2009-01-02.
3. Lakes, R.S. (1987-02-27), "Foam structures with a negative Poisson's ratio", Science, 235 (4792): 1038–40, Bibcode:1987Sci...235.1038L, doi:10.1126/science.235.4792.1038, PMID 17782252.
4. Evans, Ken (1991), "Auxetic polymers: a new range of materials", Endeavour, 15: 170–174, doi:10.1016/0160-9327(91)90123-S.
5. Kolpakov, A.G. "Determination of the average characteristics of elastic frameworks". Journal of Applied Mathematics and Mechanics. 49 (6): 739–745. Bibcode:1985JApMM..49..739K. doi:10.1016/0021-8928(85)90011-5.
6. Almgren, R.F. (1985). "An isotropic three-dimensional structure with Poisson's ratio=-1". J. Elasticity. 15: 427–430. doi:10.1007/bf00042531.
7. Theocaris, P.S.; Stavroulakis, G.E.; Panagiotopoulos, P.D. (1997). "Negative Poisson's ratio in composites with star-shaped inclusions: a numerical homogenization approach .". Archive of Applied Mechanics. 67 (4): 274–286. Bibcode:1997AAM....67..274T. doi:10.1007/s004190050117.
8. Theocaris, P.S.; Stavroulakis, G.E. "The homogenization method for the study of variation of Poisson's ratio in fiber composites". Archive of Applied Mechanics. 69 (3-4): 281–295.
9. Stavroulakis, G.E. "Auxetic behaviour: Appearance and engineering applications". Physica Status Solidi (b). 242 (3): 710–720. Bibcode:2005PSSBR.242..710S. doi:10.1002/pssb.200460388.
10. Kaminakis, N.T.; Stavroulakis, G.E. "Topology optimization for compliant mechanisms, using evolutionary-hybrid algorithms and application to the design of auxetic materials". Composites Part B: Engineering. 43 (6): 2655–2668. doi:10.1016/j.compositesb.2012.03.018.
11. A stretch of the imagination - 7 June 1997 - New Scientist Space
12. Li, Yan; Zeng, Changchun (2016). "On the successful fabrication of auxetic polyurethane foams: Materials requirement, processing strategy and conversion mechanism". Polymer. 87: 98–107. doi:10.1016/j.polymer.2016.01.076.
13. Li, Yan; Zeng, Changchun (2016). "Room‐Temperature, Near‐Instantaneous Fabrication of Auxetic Materials with Constant Poisson's Ratio over Large Deformation". Advanced Materials. 28 (14): 2822–2826. doi:10.1002/adma.201505650.
14. Burke, Maria (1997-06-07), "A stretch of the imagination", New Scientist, 154 (2085): 36
15. Grima, J. N.; Winczewski, S.; Mizzi, L.; Grech, M. C.; Cauchi, R.; Gatt, R.; Attard, D.; Wojciechowski, K.W.; Rybicki, J. (2014). "Tailoring Graphene to Achieve Negative Poisson's Ratio Properties". Advanced Materials. 27: 1455–1459. doi:10.1002/adma.201404106.
16. Gatt R, Vella Wood M, Gatt A, Zarb F, Formosa C, Azzopardi KM, Casha A, Agius TP, Schembri-Wismayer P, Attard L, Chockalingam N, Grima JN (2015). "Negative Poisson's ratios in tendons: An unexpected mechanical response". Acta Biomater. 24: 201–208. doi:10.1016/j.actbio.2015.06.018.
17. Auxetic materials, retrieved 2009-01-02.
18. Baum et al. 1984, Tappi journal, Öhrn, O. E. (1965): Thickness variations of paper on stretching, Svensk Papperstidn. 68(5), 141.
19. Verma, Prateek; Shofner, ML; Griffin, AC (2013). "Deconstructing the auxetic behavior of paper". Physica Status Solidi B. 251 (2): 289–296. Bibcode:2014PSSBR.251..289V. doi:10.1002/pssb.201384243.
20. Mark, Schenk (2011). Folded Shell Structures, PhD Thesis (PDF). University of Cambridge, Clare College.
21. http://www.nature.com/articles/srep05979
22. Eidini, Maryam; Paulino, Glaucio H. (2015). "Unraveling metamaterial properties in zigzag-base folded sheets". Science Advances. 1 (8): e1500224. arXiv:1502.05977. Bibcode:2015SciA....1E0224E. doi:10.1126/sciadv.1500224. ISSN 2375-2548.
23. Tiemo Bückmann; et al. (May 2012). "Tailored 3D Mechanical Metamaterials Made by Dip-in Direct-Laser-Writing Optical Lithography". Advanced Materials. 24: 2710–2714. doi:10.1002/adma.201200584. PMID 22495906. Retrieved 10 May 2012.
24. Stetsenko, M (2015). "Determining the elastic constants of hydrocarbons of heavy oil products using molecular dynamics simulation approach". Journal of Petroleum Science and Engineering. 126: 124–130. doi:10.1016/j.petrol.2014.12.021.
25. Verma, Prateek; Lin, A; Wagner, KB; Shofner, ML; Griffin, AC (2015). "Inducing out-of-plane auxetic behavior in needle-punched nonwovens". Physica Status Solidi B. 252 (7): 1455–1464. Bibcode:2015PSSBR.252.1455V. doi:10.1002/pssb.201552036.
26. Webb, Jonathan (16 March 2016). "Islamic art inspires stretchy, switchable materials". British Broadcasting Corporation. Retrieved 16 March 2016.

External links

• Materials with negative Poisson's ratio
• Auxetic foam in youtube
• General Information about Auxetic Materials