Catalan surface
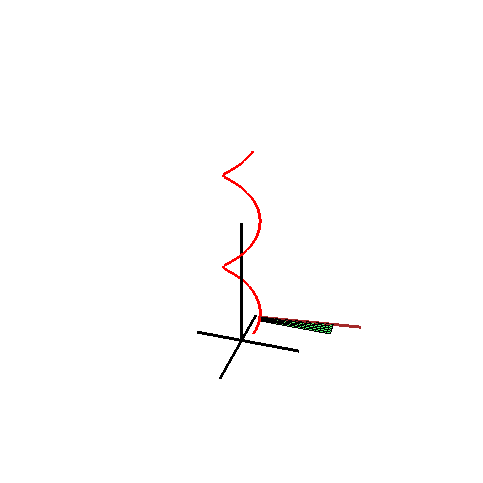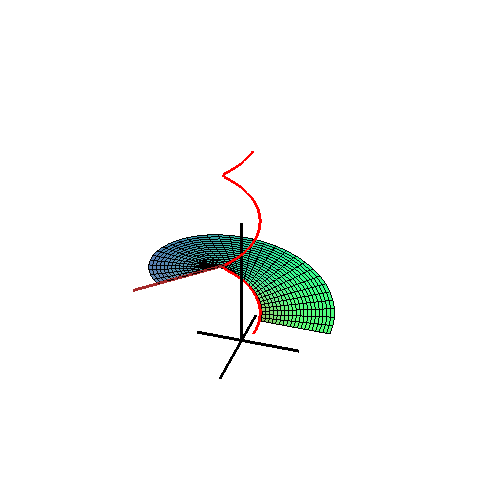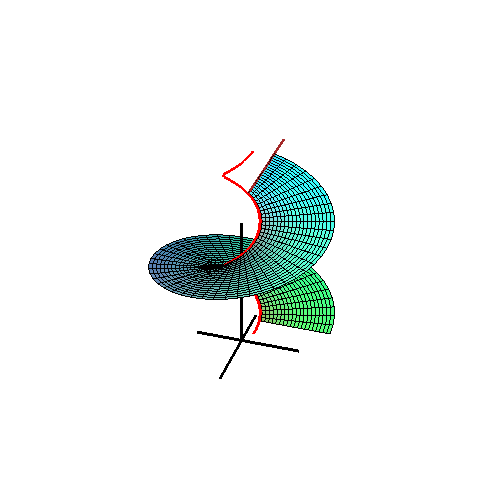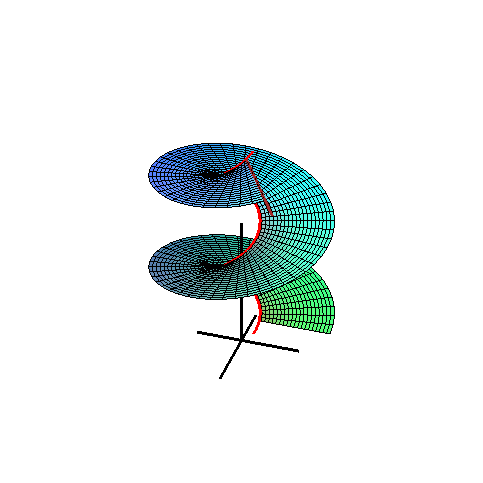
A Catalan surface.
This article is about the ruled surfaces. For the minimal surface, see Catalan's minimal surface.
In geometry, a Catalan surface, named after the Belgian mathematician Eugène Charles Catalan, is a ruled surface all of whose rulings are parallel to a fixed plane.
Equations
The vector equation of a Catalan surface is given by
- r = s(u) + v L(u),
where r = s(u) is the space curve and L(u) is the unit vector of the ruling at u = u. All the vectors L(u) are parallel to the same plane, called the directrix plane of the surface. This can be characterized by the condition: the mixed product [L(u), L' (u), L" (u)] = 0.
The parametric equations of the Catalan surface are
Special cases
If all the rulings of a Catalan surface intersect a fixed line, then the surface is called a conoid.
Catalan proved that the helicoid and the plane were the only ruled minimal surfaces.
See also
References
- A. Gray, E. Abbena, S. Salamon, Modern differential geometry of curves and surfaces with Mathematica, 3rd ed. Boca Raton, FL:CRC Press, 2006. (ISBN 978-1-58488-448-4)
- Hazewinkel, Michiel, ed. (2001), "Catalan surface", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- V. Y. Rovenskii, Geometry of curves and surfaces with MAPLE (ISBN 978-0-8176-4074-3)
This article is issued from Wikipedia - version of the 10/21/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.