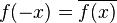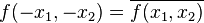Hermitian function
In mathematical analysis, a Hermitian function is a complex function with the property that its complex conjugate is equal to the original function with the variable changed in sign:
(where the overbar indicates the complex conjugate) for all 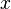 in the domain of
in the domain of 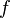 .
.
This definition extends also to functions of two or more variables, e.g., in the case that 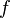 is a function of two variables it is Hermitian if
is a function of two variables it is Hermitian if
for all pairs 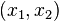 in the domain of
in the domain of  .
.
From this definition it follows immediately that: 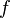 is a Hermitian function if and only if
is a Hermitian function if and only if
- the real part of
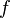 is an even function,
is an even function, - the imaginary part of
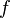 is an odd function.
is an odd function.
Motivation
Hermitian functions appear frequently in mathematics, physics, and signal processing. For example, the following two statements follow from basic properties of the Fourier transform:
- The function
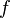 is real-valued if and only if the Fourier transform of
is real-valued if and only if the Fourier transform of 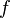 is Hermitian.
is Hermitian. - The function
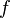 is Hermitian if and only if the Fourier transform of
is Hermitian if and only if the Fourier transform of 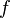 is real-valued.
is real-valued.
Since the Fourier transform of a real signal is guaranteed to be Hermitian, it can be compressed using the Hermitian even/odd symmetry. This, for example, allows the discrete Fourier transform of a signal (which is in general complex) to be stored in the same space as the original real signal.
- If f is Hermitian, then
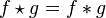 .
.
Where the 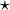 is cross-correlation, and
is cross-correlation, and 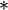 is convolution.
is convolution.
- If both f and g are Hermitian, then
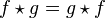 .
.